题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为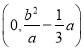 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存在
,是否存在![]() 使得
使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)写出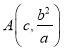 ,根据
,根据![]() ,斜率乘积为-1,建立等量关系求解离心率;
,斜率乘积为-1,建立等量关系求解离心率;
(2)写出直线AB的方程,根据韦达定理求出点B的坐标,计算出弦长![]() ,根据垂直关系同理可得
,根据垂直关系同理可得![]() ,利用等式
,利用等式![]() 即可得解.
即可得解.
(1)由题可得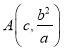 ,过点
,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为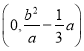 ,
,
![]() 即
即![]() ,
,
![]() ,
,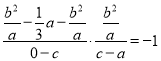
化简得:![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以![]() ;
;
(2)椭圆![]() 的方程为
的方程为![]() ,
,
由(1)可得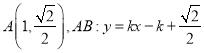 ,
,![]()
联立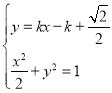 得:
得:![]() ,
,
设B的横坐标![]() ,根据韦达定理
,根据韦达定理![]() ,
,
即![]() ,
,![]() ,
,
所以![]() ,
,
同理可得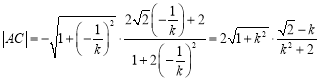
若存在![]() 使得
使得![]() 成立,
成立,
则![]() ,
,
化简得:![]() ,
,![]() ,此方程无解,
,此方程无解,
所以不存在![]() 使得
使得![]() 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
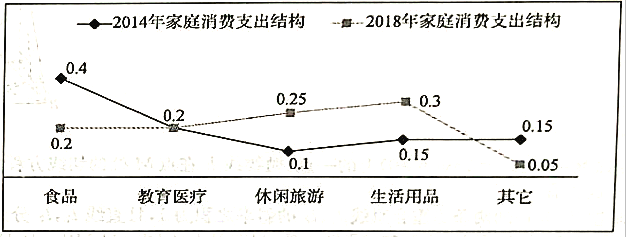
小学生10分钟应用题系列答案【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为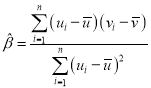 ,
,![]()
【题目】据历年大学生就业统计资料显示:某大学理工学院学生的就业去向涉及公务员、教师、金融、公司和自主创业等五大行业2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业,毕业生人数分别是70人,140人和210人现采用.分层抽样的方法,从该学院毕业生中抽取18人调查学生的就业意向.
(1)应从该学院三个专业的毕业生中分别抽取多少人?
(2)国家鼓励大学生自主创业,在抽取的18人中,就业意向恰有三个行业的学生有5人为方便统计,将恰有三个行业就业意向的这5名学生分别记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,统计如下表:
,统计如下表:
|
|
|
|
| |
公务员 | ○ | ○ | × | ○ | × |
教师 | ○ | × | ○ | × | ○ |
金融 | ○ | ○ | ○ | × | ○ |
公式 | × | × | ○ | ○ | ○ |
自主创业 | × | ○ | ○ | × |
其中“○”表示有该行业就业意向,“×”表示无该行业就业意向.
现从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这5人中随机抽取2人接受采访.设
这5人中随机抽取2人接受采访.设![]() 为事件“抽取的2人中至少有一人有自主创业意向”,求事件
为事件“抽取的2人中至少有一人有自主创业意向”,求事件![]() 发生的概率.
发生的概率.
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.