题目内容
已知数列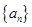 前n项和为
前n项和为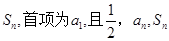 成等差数列.
成等差数列.
(I)求数列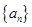 的通项公式;
的通项公式;
(II)数列满足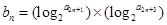 ,求证:
,求证: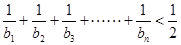 .
.
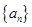 前n项和为
前n项和为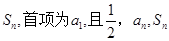 成等差数列.
成等差数列.(I)求数列
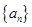 的通项公式;
的通项公式;(II)数列满足
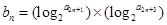 ,求证:
,求证: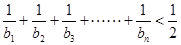 .
.(I)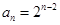 ;(II)详见解析.
;(II)详见解析.
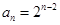 ;(II)详见解析.
;(II)详见解析.试题分析:(I)由
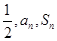 成等差数列得到
成等差数列得到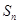 与
与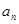 的关系,令
的关系,令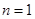 可求出
可求出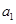 .利用
.利用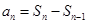 可得
可得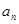 的递推公式,在本题中由此即可得出
的递推公式,在本题中由此即可得出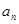 是等比数列,从而可得其通项公式;(II)由第一问并通过对数的运算性质将
是等比数列,从而可得其通项公式;(II)由第一问并通过对数的运算性质将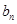 化简.得到
化简.得到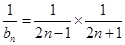 ,通过裂项
,通过裂项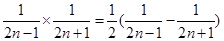 ,由裂项相消法即可得到
,由裂项相消法即可得到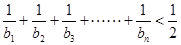 .
.试题解析:(I)
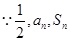 成等差数列,
成等差数列, 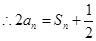 1分
1分当
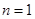 时,
时,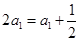 ,
,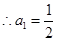 2分
2分当
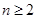 时,
时,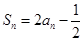 ,
,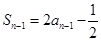 ,
,两式相减得:
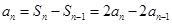 ,
,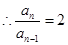 5分
5分所以数列
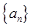 是首项为
是首项为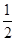 ,公比为2的等比数列,
,公比为2的等比数列,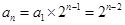 7分
7分(II)
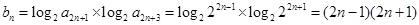 9分
9分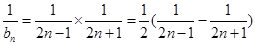 11分
11分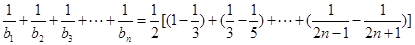
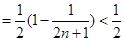 14分
14分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
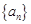 的前n项和为Sn,且
的前n项和为Sn,且 .
.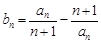 ,记数列
,记数列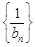 的前
的前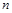 项和为
项和为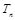 .求证:
.求证: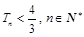 .
.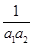 +
+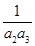 +…+
+…+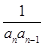 <
<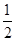 .
.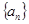 满足
满足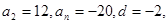 则
则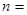 ( )
( )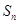 是等差数列
是等差数列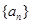 的前
的前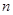 项和,若
项和,若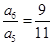 ,则
,则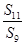 =( )
=( )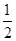
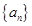 满足
满足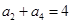 ,
,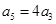 ,则数列
,则数列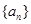 满足
满足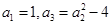 ,则
,则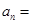 .
. 为等差数列
为等差数列 的前n项和,若
的前n项和,若 ,则
,则 = .
= .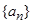 中,若
中,若 ,则
,则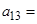 .
.