题目内容
设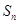 是等差数列
是等差数列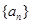 的前
的前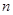 项和,若
项和,若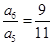 ,则
,则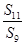 =( )
=( )
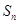 是等差数列
是等差数列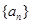 的前
的前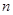 项和,若
项和,若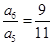 ,则
,则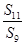 =( )
=( )| A.1 | B.-1 | C.2 | D.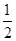 |
A
试题分析:因为
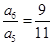 ,由等差数列前
,由等差数列前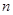 项和公式得,
项和公式得,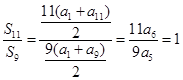 ,选A.
,选A.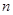 项和公式;2.等差数列的性质,对任意的
项和公式;2.等差数列的性质,对任意的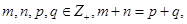 则
则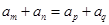 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
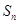 是等差数列
是等差数列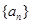 的前
的前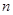 项和,若
项和,若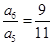 ,则
,则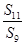 =( )
=( )| A.1 | B.-1 | C.2 | D.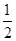 |
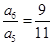 ,由等差数列前
,由等差数列前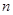 项和公式得,
项和公式得,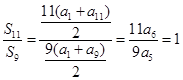 ,选A.
,选A.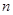 项和公式;2.等差数列的性质,对任意的
项和公式;2.等差数列的性质,对任意的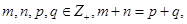 则
则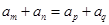 .
.
 名校课堂系列答案
名校课堂系列答案