题目内容
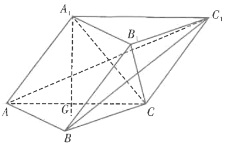
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,以
,以![]() ,
,![]() ,
,![]() 和
和![]() 为顶点的梯形的高为
为顶点的梯形的高为![]() ,面积为
,面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意两点,若直线
上的任意两点,若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由梯形![]() 的高求出
的高求出![]() ,由梯形
,由梯形![]() 的面积,建立关于
的面积,建立关于![]() 方程,结合
方程,结合![]() 关系,即可求出椭圆标准方程;
关系,即可求出椭圆标准方程;
(2)设直线![]() 的方程为:
的方程为:![]() ,利用直线与圆
,利用直线与圆![]() 相切,得到
相切,得到![]() 关系,直线方程与椭圆方程联立,设
关系,直线方程与椭圆方程联立,设![]() ,
,![]() ,得出
,得出![]() 关系,由相交弦长公式,求出
关系,由相交弦长公式,求出![]() 关于
关于![]() 的函数,根据函数特征,求出其范围,再由
的函数,根据函数特征,求出其范围,再由![]() ,即可求出结论.
,即可求出结论.
(1)由题意,得![]() ,且
,且![]() ,
,
∴![]() ,又
,又![]() ,解得
,解得![]() ,
,![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
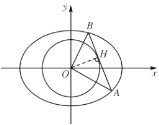
(2)如图,设![]() ,
,![]() ,
,
当圆![]() 的切线
的切线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为:
的方程为:![]() ,
,
切点为![]() ,连结
,连结![]() ,则
,则![]() .
.
因为![]() 与圆
与圆![]() 相切,
相切,
所以![]() ,所以
,所以![]() .
.
联立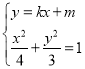 ,整理得
,整理得![]() .
.
![]()
![]()
所以![]() ,
,![]() .
.
又![]()
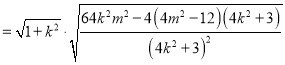
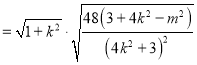
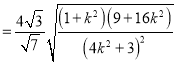
![]() .
.
①若![]() 时,
时,
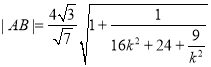 .
.
因为![]() ,
,
当且仅当![]() 时,“
时,“![]() ”成立.
”成立.
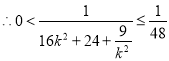
所以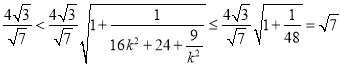
即![]() .
.
②当![]() 时,
时,![]() ,所以
,所以![]() .
.
又![]() ,
,
所以![]() .
.
当圆![]() 的切线斜率不存在时,则
的切线斜率不存在时,则![]() 的方程为
的方程为![]() 或
或![]() .
.
此时![]() ,
,![]() 的坐标分别为
的坐标分别为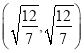 ,
, 或
或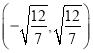 ,
,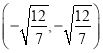 .此时
.此时![]() .
.
综上,![]() 面积的取值范围为
面积的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
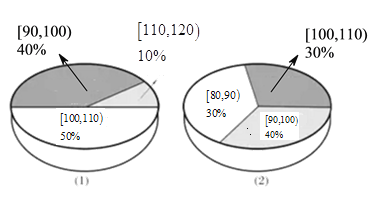
小学生10分钟应用题系列答案【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
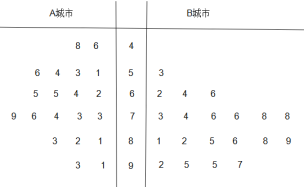
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方式“不认可”.
(Ⅰ)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关?
认可 | 不认可 | 合计 | |
A城市 | |||
B城市 | |||
合计 |
(Ⅱ)在样本A,B两个城市对此教育机构授课方式“认可”的用户中按分层抽样的方法抽取6人,若在此6人中任选2人参加数学竞赛,求A城市中至少有1人参加的概率.
参考公式: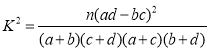 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |