题目内容
【题目】已知定圆![]() :
:![]() ,动圆
,动圆![]() 过点
过点![]() ,且和圆
,且和圆![]() 相切.
相切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() :
:![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线经过点
的垂直平分线经过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)圆![]() 的半径
的半径![]() ,设动圆
,设动圆![]() 的半径为
的半径为![]() 由
由![]() ,从而圆
,从而圆![]() 内切于圆
内切于圆![]() ,根据
,根据![]() ,利用椭圆的定义可得
,利用椭圆的定义可得![]() ,
,![]() ,从而求出椭圆的方程.
,从而求出椭圆的方程.
(Ⅱ)将直线与椭圆联立消去![]() 得到
得到![]() ,
,![]() ,即
,即![]() ,设
,设![]() ,
,![]() ,利用韦达定理求出弦
,利用韦达定理求出弦![]() 中点
中点![]() 的坐标,线段
的坐标,线段![]() 的垂直平分线方程是
的垂直平分线方程是![]() ,将点
,将点![]() 代入整理可得
代入整理可得![]() ,代入
,代入![]() 即可求解.
即可求解.
(Ⅰ)圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
设动圆![]() 的半径为
的半径为![]() ,依题意有
,依题意有![]() .
.
由![]() ,可知点
,可知点![]() 在圆
在圆![]() 内,从而圆
内,从而圆![]() 内切于圆
内切于圆![]() ,故
,故![]() ,
,
即![]() .
.
所以动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 、
、![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆.
的椭圆.
因为![]() ,
,![]() ,所以
,所以![]() .
.
于是![]() 的方程是
的方程是![]() .
.
(Ⅱ)设![]() ,
,![]() ,联立
,联立 消去
消去![]() 得到,
得到,
![]() ,即
,即![]() .
.
则![]() ,
,![]() ,
,
弦![]() 中点
中点![]() 的坐标是
的坐标是![]() .
.
由![]() ,得
,得![]() .
.
另一个方面,线段![]() 的垂直平分线方程是
的垂直平分线方程是![]() .
.
点![]() 在此直线上,
在此直线上,
得到![]() ,整理得
,整理得![]() .
.
代入![]() 中,
中,![]() ,
,![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
故实数![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (b,c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b,c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(1)现从抽取的6件合格产品中再任选2件,求选中的2件均为优等品的概率;
(2)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
根据所给统计量,求y关于x的回归方程.
附:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: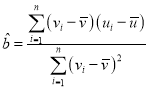 ,
,![]() ,
,![]() .
.
