题目内容
【题目】△ABC中A(3,﹣1),AB边上的中线CM所在直线方程为6x+10y﹣59=0,∠B的平分线方程BT为x﹣4y+10=0.
(1)求顶点B的坐标;
(2)求直线BC的方程.
【答案】
(1)解:设B(x0,y0),则AB的中点M( ![]() ,
, ![]() )在直线CM上.
)在直线CM上.
∴ ![]() ,
,
∴3x0+5y0+4﹣59=0,
即3x0+5y0﹣55=0,①
又点B在直线BT上,则x0﹣4y0+10=0,②
由①②可得x0=10,y0=5,即B点的坐标为(10,5).
(2)解:设点A(3,﹣1)关于直线BT的对称点D的坐标为(a,b),
则点D在直线BC上.
由题知 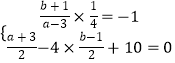 ,
,
得 ![]() ,∴D(1,7).(7分)
,∴D(1,7).(7分)
kBC=kBD= ![]() =﹣
=﹣ ![]() ,(8分)
,(8分)
∴直线BC的方程为y﹣5=﹣ ![]() ,即2x+9y﹣65=0.
,即2x+9y﹣65=0.
【解析】(1)设B(x0 , y0),则AB的中点M( ![]() ,
, ![]() )在直线CM上,从而3x0+5y0﹣55=0,又点B在直线BT上,则x0﹣4y0+10=0,由此能求出B点的坐标.(2)设点A(3,﹣1)关于直线BT的对称点D的坐标为(a,b),则点D在直线BC上,从而D(1,7),由此能求出直线BC的方程.
)在直线CM上,从而3x0+5y0﹣55=0,又点B在直线BT上,则x0﹣4y0+10=0,由此能求出B点的坐标.(2)设点A(3,﹣1)关于直线BT的对称点D的坐标为(a,b),则点D在直线BC上,从而D(1,7),由此能求出直线BC的方程.
【考点精析】认真审题,首先需要了解直线的斜率(一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα).

练习册系列答案
相关题目