题目内容
(12分)
已知直线过点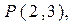 且在两坐标轴上的截距的绝对值相等,求直线的方程。
且在两坐标轴上的截距的绝对值相等,求直线的方程。
直线方程为:
解析

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
设集合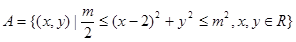 ,
, , 若
, 若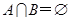 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.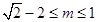 | B.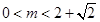 |
C.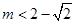 或 或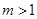 | D.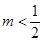 或 或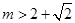 |
题目内容
(12分)
已知直线过点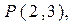 且在两坐标轴上的截距的绝对值相等,求直线的方程。
且在两坐标轴上的截距的绝对值相等,求直线的方程。
直线方程为:
解析

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案设集合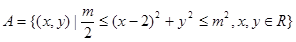 ,
, , 若
, 若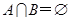 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.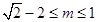 | B.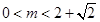 |
C.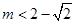 或 或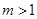 | D.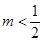 或 或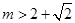 |