题目内容
(满分12分)
设直线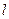 的方程为
的方程为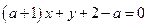
 。
。
(1)若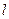 在两坐标轴上的截距相等
在两坐标轴上的截距相等 ,求
,求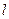 的方程;
的方程;
(2)若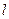 不经过第二象限,求
不经过第二象限,求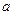 的取值范围。
的取值范围。
(1)
(2)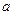 的取值范围是
的取值范围是
解析

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
题目内容
(满分12分)
设直线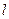 的方程为
的方程为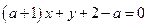
 。
。
(1)若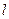 在两坐标轴上的截距相等
在两坐标轴上的截距相等 ,求
,求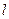 的方程;
的方程;
(2)若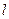 不经过第二象限,求
不经过第二象限,求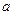 的取值范围。
的取值范围。
(1)
(2)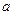 的取值范围是
的取值范围是
解析

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案