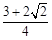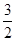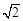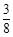题目内容
设A为圆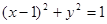 上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是( )
上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是( )
A.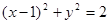 | B.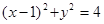 |
C.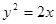 | D.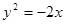 |
A
解析试题分析:设圆已知圆的圆心为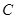 ,则
,则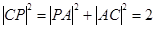 ,所以点
,所以点 在以圆
在以圆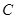 为圆心,
为圆心,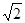 为半径的圆上,则P点的轨迹方程是
为半径的圆上,则P点的轨迹方程是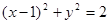 。
。
考点:利用定义法求曲线的轨迹方程。

练习册系列答案
相关题目
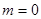 是方程
是方程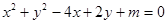 表示圆的( )条件
表示圆的( )条件
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
若圆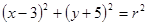 上的点到直线
上的点到直线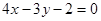 的最近距离等于1,则半径
的最近距离等于1,则半径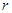 的值为( )
的值为( )
A.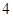 | B.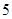 | C.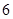 | D.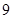 |
已知条件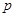 :
: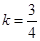 ,条件
,条件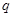 :直线
:直线 与圆
与圆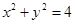 相切,则
相切,则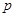 是
是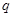 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
| A.(x-2)2+(y-1)2=1 | B.(x-2)2+(y-3)2=1 |
| C.(x-3)2+(y-2)2=1 | D.(x-3)2+(y-1)2=1 |
如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则( )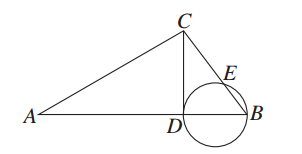
| A.CE·CB=AD·DB | B.CE·CB=AD·AB |
| C.AD·AB=CD2 | D.CE·EB=CD2 |
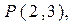 且在两坐标轴上的截距的绝对值相等,求直线的方程。
且在两坐标轴上的截距的绝对值相等,求直线的方程。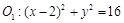 和圆
和圆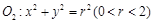 ,动圆M与圆
,动圆M与圆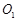 ,圆
,圆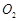 都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为
都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为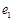 ,
,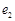 (
(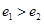 ),则
),则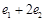 的最小值是( )
的最小值是( )