题目内容
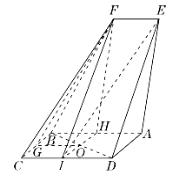
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求多面体![]() 的体积.
的体积.
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)证明线面平行可证明直线平行于平面内的直线,本题中只需证明![]() ;(2)证明面面垂直可证明其中一个平面经过另外一个平面的垂线,本题中只需证明平面
;(2)证明面面垂直可证明其中一个平面经过另外一个平面的垂线,本题中只需证明平面![]() 中的
中的![]() 平面
平面![]() ;(3)不规则多面体的体积求解时将其分割为柱体和椎体分别求体积
;(3)不规则多面体的体积求解时将其分割为柱体和椎体分别求体积
试题解析:(1)证明:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
在![]() 中,∵
中,∵![]() 是
是![]() 的中点,
的中点,
∴![]() 且
且![]() ,又∵
,又∵![]() ,∴
,∴![]() 且
且![]() ,即四边形
,即四边形![]() 是平行四边形,∴.又
是平行四边形,∴.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)证明:在![]() 中,
中,![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,∵
,∵![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]()
![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)解:连![]() ,并延长交
,并延长交![]() 于
于![]() ,连
,连![]() .
.
∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() 是
是![]() 中点,∵
中点,∵![]() ,
,![]() ,
,
∴多面体![]() 为三棱柱,体积为
为三棱柱,体积为![]() ,且四边形
,且四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,
,
∴多面体![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】某校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的55名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选2人,求恰有1个男生和1个女生的概率.
临界值参考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)