题目内容
已知一几何体的直观图和三视图如下图示: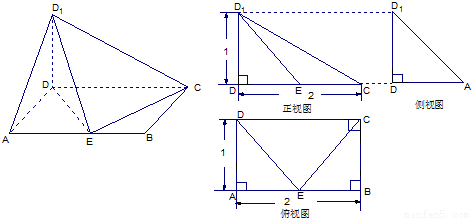
假设点E是AB上的动点,试根据以上图形提供的信息解决以下问题.
(1)三棱锥C-DED1的体积是否与点E的位置有关?说明理由;
(2)当异面直线AD1与EC所成角为60°时,请确定动点E的位置;
(3)在(2)的条件下,求证平面DED1⊥平面D1EC.
【答案】分析:(1)三棱锥C-DED1的体积与点E的位置无关,因为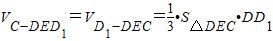 ,所以不论点E在AB上的任何位置都有
,所以不论点E在AB上的任何位置都有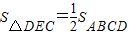 ,所以三棱锥的体积为定值.
,所以三棱锥的体积为定值.
(2)作AE'∥CE交CD于E',可得AE'=D1E',进而得到AD1E'为正三角形,所以AE=DE'=1,这时点E为AB的中点.
(3)由(2)知,E为AB的中点,所以∠AED=∠BEC=45°所以CE⊥DE,由题意可得CE⊥DD1,DE∩DD1=D,所以CE⊥平面D1ED.进而得到面面垂直.
解答:解:由该几何体的三视图知,ABCD为矩形,D1D⊥平面ABCD,AD=DD1=1,AB=2.
(1)三棱锥C-DED1的体积与点E的位置无关,
这是∵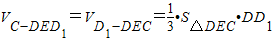
∵不论点E在AB上的任何位置都有
∴不论点E在AB上的任何位置都有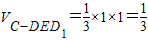
(2)作AE'∥CE交CD于E',
∵AD=DD1=1,∴AE'=D1E',
又异面直线AD1与EC所成角为60,∴△AD1E'为正三角形,
从而AE=DE'=1,这时点E为AB的中点.
(3)由(2)知,E为AB的中点,∴△DAE与△EBC都是等腰直角三角形
∴∠AED=∠BEC=45°∴CE⊥DE,
又∵D1D⊥平面ABCD,EC?平面ABCD
∴CE⊥DD1,DE∩DD1=D
∴CE⊥平面D1ED
∵EC?平面D1EC
∴平面DED1⊥平面D1EC.
点评:解决三棱锥的体积问题关键是找到其膏与底面,对于动点问题一般先找线段的端点或线段的中点,证明面面垂直的方法是在其中一个平面内找另一个平面的垂线即可,此类题目在高考中经常以解答题的形式出现.
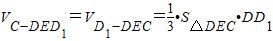 ,所以不论点E在AB上的任何位置都有
,所以不论点E在AB上的任何位置都有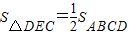 ,所以三棱锥的体积为定值.
,所以三棱锥的体积为定值.(2)作AE'∥CE交CD于E',可得AE'=D1E',进而得到AD1E'为正三角形,所以AE=DE'=1,这时点E为AB的中点.
(3)由(2)知,E为AB的中点,所以∠AED=∠BEC=45°所以CE⊥DE,由题意可得CE⊥DD1,DE∩DD1=D,所以CE⊥平面D1ED.进而得到面面垂直.
解答:解:由该几何体的三视图知,ABCD为矩形,D1D⊥平面ABCD,AD=DD1=1,AB=2.
(1)三棱锥C-DED1的体积与点E的位置无关,
这是∵
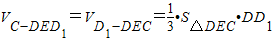
∵不论点E在AB上的任何位置都有

∴不论点E在AB上的任何位置都有
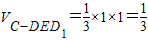
(2)作AE'∥CE交CD于E',
∵AD=DD1=1,∴AE'=D1E',
又异面直线AD1与EC所成角为60,∴△AD1E'为正三角形,
从而AE=DE'=1,这时点E为AB的中点.
(3)由(2)知,E为AB的中点,∴△DAE与△EBC都是等腰直角三角形
∴∠AED=∠BEC=45°∴CE⊥DE,
又∵D1D⊥平面ABCD,EC?平面ABCD
∴CE⊥DD1,DE∩DD1=D
∴CE⊥平面D1ED
∵EC?平面D1EC
∴平面DED1⊥平面D1EC.
点评:解决三棱锥的体积问题关键是找到其膏与底面,对于动点问题一般先找线段的端点或线段的中点,证明面面垂直的方法是在其中一个平面内找另一个平面的垂线即可,此类题目在高考中经常以解答题的形式出现.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
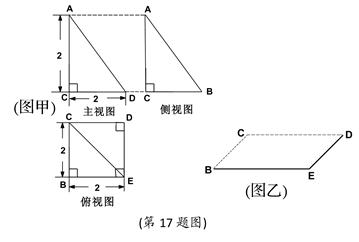
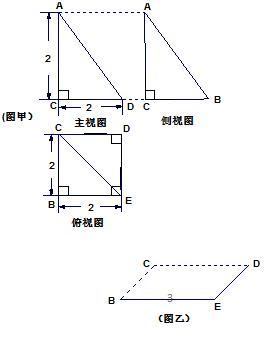 已知一几何体的三视图如图(甲)示,(三视图中已经给出各投影面顶点的标记)
已知一几何体的三视图如图(甲)示,(三视图中已经给出各投影面顶点的标记)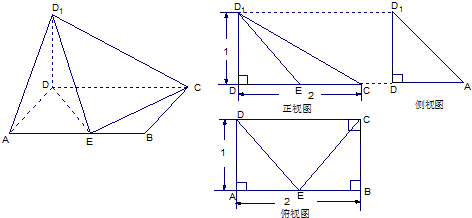

 面ABE;
面ABE;