题目内容
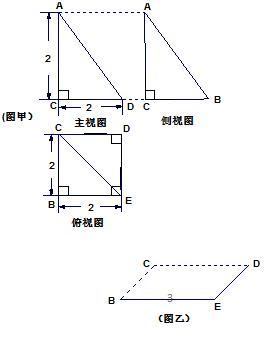 已知一几何体的三视图如图(甲)示,(三视图中已经给出各投影面顶点的标记)
已知一几何体的三视图如图(甲)示,(三视图中已经给出各投影面顶点的标记)(1)在已给出的一个面上(图乙),画出该几何体的直观图;
(2)设点F、H、G分别为AC,AD,DE的中点,
求证:FG∥平面ABE;
(3)求该几何体的全面积.
分析:(1)根据三视图判断该几何体是底面为正方形的直四棱柱,AC垂直底面.
(2)利用三角形的中位线性质证明线面平行,进而证明面面平行,再利用面面平行的性质证明线面平行.
(3)棱锥的全面积等与各个面的面积之和,先证各个侧面都是直角三角形,计算出各个侧面的面积.
(2)利用三角形的中位线性质证明线面平行,进而证明面面平行,再利用面面平行的性质证明线面平行.
(3)棱锥的全面积等与各个面的面积之和,先证各个侧面都是直角三角形,计算出各个侧面的面积.
解答: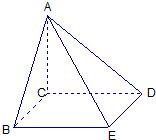 解:(1)该几何体的直观图如图示:
解:(1)该几何体的直观图如图示:
(2)证明:由图(甲)知四边形CBED为正方形
∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE
同理可得 HG∥面ABE
又∵FH∩HG=H
∴平面FHG∥平面ABE
又∵FG?面FHG
∴FG∥平面ABE
(3)由图甲知AC⊥CD,AC⊥BC,BC⊥CD
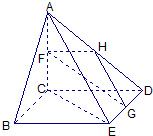 ∴CD⊥平面ACB,
∴CD⊥平面ACB,
∴CD⊥AB
同理可得ED⊥AD
∵S△ACB=S△ACD,S△ABE=S△ADE=
×2×2
=2
,SCBED=4,
∴该几何体的全面积
S=S△ACB+S△ACD+S△ABE+S△ADE+SCBED=2+2+4
+4=4(2+
).
 解:(1)该几何体的直观图如图示:
解:(1)该几何体的直观图如图示:(2)证明:由图(甲)知四边形CBED为正方形
∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE
同理可得 HG∥面ABE
又∵FH∩HG=H
∴平面FHG∥平面ABE
又∵FG?面FHG
∴FG∥平面ABE
(3)由图甲知AC⊥CD,AC⊥BC,BC⊥CD
 ∴CD⊥平面ACB,
∴CD⊥平面ACB,∴CD⊥AB
同理可得ED⊥AD
∵S△ACB=S△ACD,S△ABE=S△ADE=
| 1 |
| 2 |
| 2 |
| 2 |
∴该几何体的全面积
S=S△ACB+S△ACD+S△ABE+S△ADE+SCBED=2+2+4
| 2 |
| 2 |
点评:本题考查利用三视图判断几何体的形状,求几何体的表面积,证明线面垂直.

练习册系列答案
相关题目
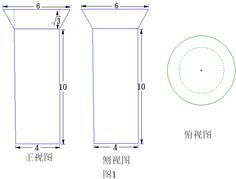 已知一几何体的三视图如图所示,则该几何体的体积为( )
已知一几何体的三视图如图所示,则该几何体的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 已知一几何体的三视图如下,其中正视图,侧视图均为矩形,俯视图为等腰直角三角形,则该几何体的体积为
已知一几何体的三视图如下,其中正视图,侧视图均为矩形,俯视图为等腰直角三角形,则该几何体的体积为 已知一几何体的三视图如图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( )
已知一几何体的三视图如图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( ) 已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.
已知一几何体的三视图如图,主视图与左视图为全等的等腰直角三角形,直角边长为6,俯视图为正方形,(1)求点A到面SBC的距离;(2)有一个小正四棱柱内接于这个几何体,棱柱底面在面ABCD内,其余顶点在几何体的棱上,当棱柱的底面边长与高取何值时,棱柱的体积最大,并求出这个最大值.