题目内容
抛物线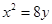 的准线与
的准线与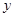 轴交于点
轴交于点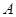 ,点
,点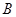 在抛物线对称轴上,过
在抛物线对称轴上,过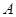 可作直线交抛物线于点
可作直线交抛物线于点 、
、 ,使得
,使得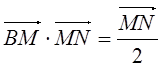 ,则
,则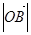 的取值范围是 .
的取值范围是 .
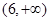
解析试题分析:由题意可得A(0,2),直线MN的斜率k存在且k≠0,设直线MN的方程为y=kx+2,
联立方程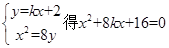 ,设M (x1,x2),N(x2,y2),MN 的中点E(x0,y0),
,设M (x1,x2),N(x2,y2),MN 的中点E(x0,y0),
则△=64k2-64>0,即k2>1,x1+x2=-8k,y1+y2=k(x1+x2)+4=4-8kk2,所以x0=-4k,y0=2-4k2即E(-4k,2-4k2).
因为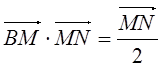 ,所以
,所以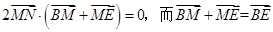
所以BE⊥MN即点B在MN的垂直平分线上,因为MN的斜率为k,E(-4k,2-4k2).所以MN的垂直平分线BE的方程为: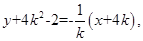 与y轴的交点即是B,令x=0可得,y=-2-4k2,
与y轴的交点即是B,令x=0可得,y=-2-4k2,
则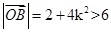 。
。
点评: 本题主要考查了向量的数量积的性质的应用,直线与抛物线的相交关系的应用,方程的根与系数关系的应用,属于向量知识的综合应用,属于难题.

练习册系列答案
相关题目

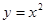 在点 处的切线平行于直线
在点 处的切线平行于直线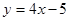 。
。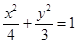 的左焦点为F,直线x=m与椭圆相交于A,B两点,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于A,B两点,当△FAB的周长最大时,△FAB的面积是 .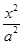 -
-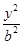 =1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________. 为左焦点,当
为左焦点,当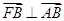 时,其离心率为
时,其离心率为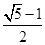 ,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 .
,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 . 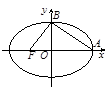
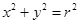 上任意一点
上任意一点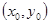 处的切线方程为:
处的切线方程为: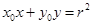 。类比以上结论有:双曲线:
。类比以上结论有:双曲线: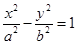 上任意一点
上任意一点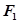 ,
,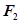 是椭圆
是椭圆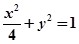 的两个焦点,点
的两个焦点,点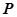 在椭圆上,且
在椭圆上,且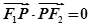 ,则△
,则△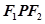 的面积为 .
的面积为 .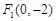 、
、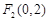 为椭圆的两个焦点,过
为椭圆的两个焦点,过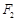 作椭圆的弦
作椭圆的弦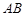 ,若
,若 的周长为
的周长为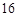 ,则该椭圆的标准方程为 .
,则该椭圆的标准方程为 .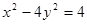 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 .