题目内容
如图,椭圆的中心在坐标原点, 为左焦点,当
为左焦点,当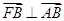 时,其离心率为
时,其离心率为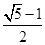 ,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 .
,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 . 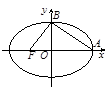
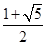
解析试题分析:在黄金双曲线中,|OA|=a,|OB|=b,|OF|=c,
由题意可知,|BF|2+|AB|2=|AF|2,
∴b2+c2+c2=a2+c2+2ac,
∵b2=c2-a2,整理得c2=a2+ac,
∴e2-e-1=0,解得 e= ,或 e=
,或 e=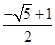 (舍去).
(舍去).
故黄金双曲线的离心率e得  .故答案为
.故答案为 .
.
考点:本题主要考查双曲线的几何性质。
点评:注意寻找黄金双曲线中a,b,c之间的关系,利用双曲线的几何性质性质求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
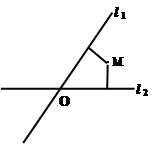
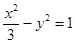 的两条渐近线的夹角大小等于 .
的两条渐近线的夹角大小等于 . 的两焦点是
的两焦点是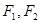 ,则其焦距长为 ,若点
,则其焦距长为 ,若点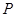 是椭圆上一点,且
是椭圆上一点,且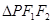 是直角三角形,则
是直角三角形,则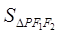 的大小是 .
的大小是 .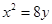 的准线与
的准线与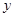 轴交于点
轴交于点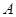 ,点
,点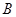 在抛物线对称轴上,过
在抛物线对称轴上,过 、
、 ,使得
,使得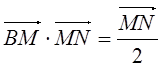 ,则
,则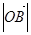 的取值范围是 .
的取值范围是 .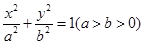 ,
,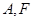 是其左顶点和左焦点,
是其左顶点和左焦点, 是圆
是圆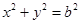 上的动点,若
上的动点,若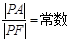 ,则此椭圆的离心率是
,则此椭圆的离心率是 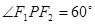 ,
,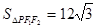 .该双曲线的标准方程为
.该双曲线的标准方程为 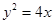 上一点
上一点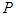 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为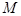 ,且
,且 ,设抛物线的焦点为
,设抛物线的焦点为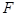 ,则
,则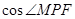 = .
= .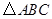 中,
中, .若以
.若以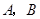 为焦点的椭圆经过点
为焦点的椭圆经过点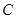 ,则该椭圆的离心率
,则该椭圆的离心率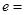 .
.