题目内容
(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为 元,则他的满意度为
元,则他的满意度为 ;如果他买进该产品的单价为
;如果他买进该产品的单价为 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为 元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1)求 和
和 关于
关于 、
、 的表达式;当
的表达式;当 时,求证:
时,求证: =
= ;
;
(2)设 ,当
,当 、
、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为 ,试问能否适当选取
,试问能否适当选取 、
、 的值,使得
的值,使得 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
按照某学者的理论,假设一个人生产某产品单件成本为
 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为 元,则他的满意度为
元,则他的满意度为 ;如果他买进该产品的单价为
;如果他买进该产品的单价为 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为
 元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1)求
 和
和 关于
关于 、
、 的表达式;当
的表达式;当 时,求证:
时,求证: =
= ;
;(2)设
 ,当
,当 、
、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为 ,试问能否适当选取
,试问能否适当选取 、
、 的值,使得
的值,使得 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。(2)即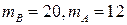 时,甲乙两人同时取到最大的综合满意度为
时,甲乙两人同时取到最大的综合满意度为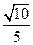 .
.
(3) 不存在满足条件的 、
、 的值
的值
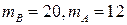 时,甲乙两人同时取到最大的综合满意度为
时,甲乙两人同时取到最大的综合满意度为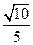 .
.(3) 不存在满足条件的
 、
、 的值
的值本小题主要考查函数的概念、基本不等式等基础知识,考查数学建模能力、抽象概括能力以及数学阅读能力。满分16分。
(1)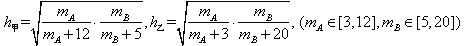
当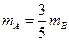 时,
时,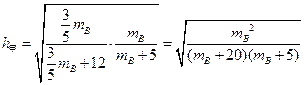 ,
,
 ,
,  =
=
(2)当 时,
时,
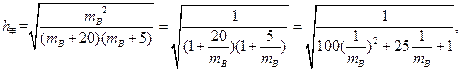
由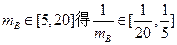 ,
,
故当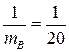 即
即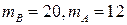 时,
时,
甲乙两人同时取到最大的综合满意度为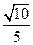 。
。
(3)(方法一)由(2)知: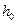 =
=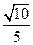
由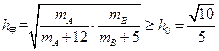 得:
得: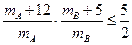 ,
,
令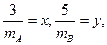 则
则 ,即:
,即: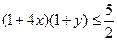 。
。
同理,由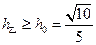 得:
得: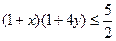
另一方面,

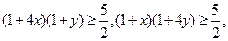 当且仅当
当且仅当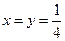 ,即
,即 =
= 时,取等号。
时,取等号。
所以不能否适当选取 、
、 的值,使得
的值,使得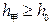 和
和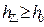 同时成立,但等号不同时成立。
同时成立,但等号不同时成立。

(1)
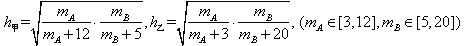
当
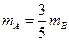 时,
时,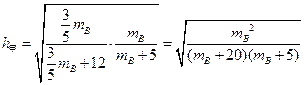 ,
, ,
,  =
=
(2)当
 时,
时,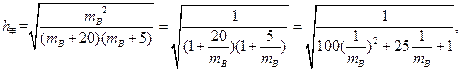
由
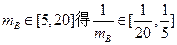 ,
,故当
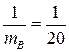 即
即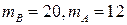 时,
时,甲乙两人同时取到最大的综合满意度为
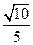 。
。(3)(方法一)由(2)知:
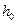 =
=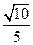
由
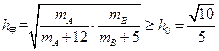 得:
得: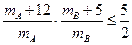 ,
,令
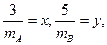 则
则 ,即:
,即: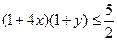 。
。同理,由
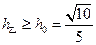 得:
得: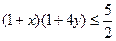
另一方面,


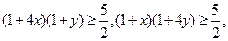 当且仅当
当且仅当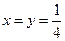 ,即
,即 =
= 时,取等号。
时,取等号。所以不能否适当选取
 、
、 的值,使得
的值,使得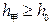 和
和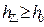 同时成立,但等号不同时成立。
同时成立,但等号不同时成立。

练习册系列答案
相关题目
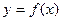
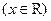 满足
满足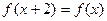 ,且
,且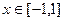 时,
时,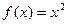 ,则
,则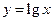 的图象的交点个数为 .
的图象的交点个数为 .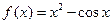 ,对于
,对于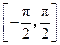 上的任意
上的任意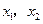 ,有如下条件
,有如下条件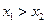 ; ②
; ②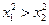 ; ③
; ③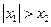 .其中能使
.其中能使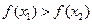 恒成立的条件序号是 .
恒成立的条件序号是 .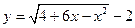
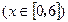 的图像绕坐标原点逆时针方向旋转角
的图像绕坐标原点逆时针方向旋转角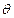
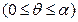 ,得到曲线
,得到曲线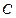 .若对于每一个旋转角
.若对于每一个旋转角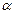 的最大值为__________
的最大值为__________
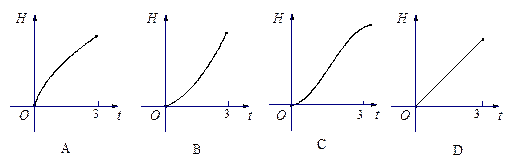 时间
时间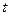 (分)的函数关系表示的图象只可能是( )
(分)的函数关系表示的图象只可能是( ) 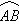 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在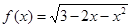 的定义域为 .
的定义域为 .