Question

【题目】已知命题p：方程表示焦点在y轴上的椭圆；命题q：椭圆（m＞0）的离心率 e∈（，1），若p∨q为真，p∧q为假，求m的取值范围．

Answer 1

【答案】（0，1]∪[2，+∞）．

【解答】解：若p为真，则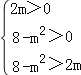，得到0＜m＜2；

若q为真，则＜＜1，即a2＜a2﹣b2＜a2，

得到﹣a2＜﹣b2＜0，于是3＜（m2+3），

可得，m＞1，

由p∨q为真，p∧q为假，可知p真q假，或p假q真．

p真q假时，得到0＜m≤1；

p假q真时，得到m≥2；

综上所述，实数m的取值范围为（0，1]∪[2，+∞）．

【解析】

试题分析:先确定p，q为真时对应m的取值范围，再根据p∨q为真，p∧q为假，可知p真q假，或p假q真．解对应方程组，求并集得m的取值范围．

试题解析:解：若p为真，则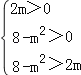，得到0＜m＜2；

若q为真，则＜＜1，即a2＜a2﹣b2＜a2，

得到﹣a2＜﹣b2＜0，于是3＜（m2+3），

可得，m＞1，

由p∨q为真，p∧q为假，可知p真q假，或p假q真．

p真q假时，得到0＜m≤1；

p假q真时，得到m≥2；

综上所述，实数m的取值范围为（0，1]∪[2，+∞）．