题目内容
已知动点P(x,y)(y≥0)到定点F(0,1)的距离和它到直线y=-1的距离相等,记点P的轨迹为曲线C.(1)求曲线C的方程;
(2)设圆M过点A(0,2),且圆心M(a,b)在曲线C上,若圆M与x轴的交点分别为E(x1,0)、G(x2,0),求线段EG的长度.
分析:(1)根据抛物线的定义可知曲线C是以F(0,1)为焦点,y=-1为准线的抛物线,进而求得p,则抛物线方程可得.
(2)表示出圆的半径,则圆的方程可得,令y=0,根据韦达定理求得x1+x2和x1•x2的表达式,进而求得(x1-x2)2,把点M代入抛物线方程求得a和b的关系,进而求得|x1-x2|的值.
(2)表示出圆的半径,则圆的方程可得,令y=0,根据韦达定理求得x1+x2和x1•x2的表达式,进而求得(x1-x2)2,把点M代入抛物线方程求得a和b的关系,进而求得|x1-x2|的值.
解答: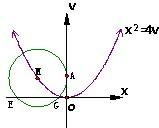 解:(1)依题意知,曲线C是以F(0,1)为焦点,y=-1为准线的抛物线
解:(1)依题意知,曲线C是以F(0,1)为焦点,y=-1为准线的抛物线
∵焦点到准线的距离p=2
∴曲线C方程是x2=4y
(2)∵圆M的半径为
∴其方程为(x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
则x1+x2=2a,x1•x2=4b-4
∴(x1-x2)2=(x1+x2)2-4x1•x2=(2a)2-4(4b-4)=4a2-16b+16
又∵点M(a,b)在抛物线x2=4y上,∴a2=4b,
∴(x1-x2)2=16,即|x1-x2|=4
∴线段EG的长度是4.
 解:(1)依题意知,曲线C是以F(0,1)为焦点,y=-1为准线的抛物线
解:(1)依题意知,曲线C是以F(0,1)为焦点,y=-1为准线的抛物线∵焦点到准线的距离p=2
∴曲线C方程是x2=4y
(2)∵圆M的半径为
| a2+(b-2)2 |
∴其方程为(x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
则x1+x2=2a,x1•x2=4b-4
∴(x1-x2)2=(x1+x2)2-4x1•x2=(2a)2-4(4b-4)=4a2-16b+16
又∵点M(a,b)在抛物线x2=4y上,∴a2=4b,
∴(x1-x2)2=16,即|x1-x2|=4
∴线段EG的长度是4.
点评:本题主要考查了圆方程得综合应用,抛物线的定义,抛物线的简单性质.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目