Question

【题目】设为实数，设函数，设

．

（1）求的取值范围，并把表示为的函数；

（2）若恒成立，求实数的取值范围；

（3）若存在使得成立，求实数的取值范围．

Answer 1

【答案】（1）取值范围是，；（2）；

（3） 。

【解析】

分析：（1）根据解析式，得出函数的定义域，将式子两边平方，结合二次函数的值域，可得的范围，进而得到；

（2）由恒成立，即有，注意到直线是抛物线的对称轴，分类讨论，得到函数的单调性，即可求得最小值，进而得到实数的取值范围.

（3）存在使得成立，即，即有且在成立，运用函数的单调性求得右边函数的最值，再由存在性问题的解法即可得到的范围.

详解：（1），

要使有意义，必须且，即，

∴，①

∴的取值范围是

由①得，

∴，；

（2）由恒成立，即有，

注意到直线是抛物线的对称轴，

分以下几种情况讨论：

①当即时，在上为递增函数，

即有时，取得最小值，且为；

②当即时，的最小值为；

③当即时，在上为递减函数，

即有时，取得最小值，且为．

则或或，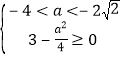

解得：或或，

则有；

（3）存在使得成立，即为

，

即有且在成立，

令，

可以得到在递减，在递增，

即有的最小值为，最大值为

即有且

则实数的取值范围是．