题目内容
已知平面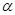 与平面
与平面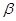 相交,直线
相交,直线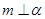 ,则( )
,则( )
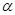 与平面
与平面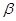 相交,直线
相交,直线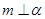 ,则( )
,则( )A.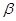 内必存在直线与 内必存在直线与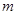 平行,且存在直线与 平行,且存在直线与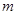 垂直 垂直 |
B.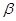 内不一定存在直线与 内不一定存在直线与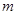 平行,不一定存在直线与 平行,不一定存在直线与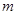 垂直 垂直 |
C.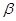 内不一定存在直线与 内不一定存在直线与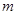 平行,但必存在直线与 平行,但必存在直线与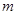 垂直 垂直 |
D.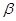 内必存在直线与 内必存在直线与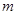 平行,不一定存在直线与 平行,不一定存在直线与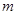 垂直 垂直 |
C
考点:
分析:作两个相交平面,交线为n,使直线m⊥α,然后利用反证法说明,假设β内一定存在直线a与m平行,根据面面垂直的判定定理证明α⊥β,这与平面α与平面β相交不一定垂直矛盾,然后根据线面垂直的性质说明β内必存在直线与m垂直,从而证得结论.
解答:解:作两个相交平面,交线为n,使直线m⊥α,
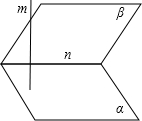 假设β内一定存在直线a与m平行,
假设β内一定存在直线a与m平行,
∵直线m⊥α,而a∥m
∴直线a⊥α,而a?β
∴α⊥β,这与平面α与平面β相交不一定垂直矛盾
∴β内不一定存在直线a与m平行;
∵直线m⊥α,n?β
∴直线m⊥直线n
∴β内必存在直线与m垂直
故选C.
点评:本题主要考查了直线与平面垂直的性质,以及面面垂直的判定,同时考查了反证法,以及推理论证的能力,属于中档题.
分析:作两个相交平面,交线为n,使直线m⊥α,然后利用反证法说明,假设β内一定存在直线a与m平行,根据面面垂直的判定定理证明α⊥β,这与平面α与平面β相交不一定垂直矛盾,然后根据线面垂直的性质说明β内必存在直线与m垂直,从而证得结论.
解答:解:作两个相交平面,交线为n,使直线m⊥α,
 假设β内一定存在直线a与m平行,
假设β内一定存在直线a与m平行,∵直线m⊥α,而a∥m
∴直线a⊥α,而a?β
∴α⊥β,这与平面α与平面β相交不一定垂直矛盾
∴β内不一定存在直线a与m平行;
∵直线m⊥α,n?β
∴直线m⊥直线n
∴β内必存在直线与m垂直
故选C.
点评:本题主要考查了直线与平面垂直的性质,以及面面垂直的判定,同时考查了反证法,以及推理论证的能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
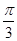 ,另一直线与这个平面所成的角是
,另一直线与这个平面所成的角是 。则这
。则这
 中,
中,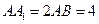 ,点
,点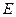 在
在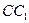 上且
上且
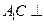 平面
平面 ;(2)求二面角
;(2)求二面角 的余弦值
的余弦值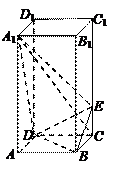
 中,
中, 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱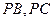 上,且
上,且 (Ⅰ)求证:
(Ⅰ)求证: 平面
平面 ;
; 的中点时,求
的中点时,求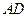 与平面
与平面 为直二面角?并说明理由.
为直二面角?并说明理由.
 中,
中,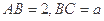 ,又
,又 ⊥平面
⊥平面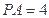 .
.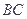 上存在一点
上存在一点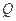 ,使
,使 ,
,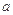 的取值范围;
的取值范围;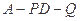 的余弦值.
的余弦值.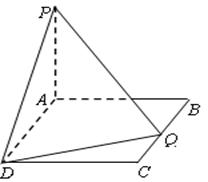
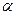 ⊥平面
⊥平面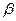 ,
,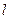 ,DA
,DA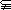
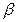 内不在
内不在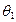 ,PC与平面
,PC与平面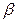 所成角为
所成角为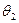 ,若
,若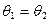 ,则△PAB的面积的最大值是 。
,则△PAB的面积的最大值是 。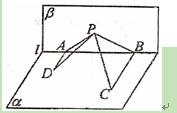
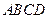 是菱形,
是菱形,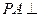 平面
平面
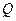 为
为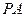 的中点.
的中点. 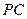 ∥平
∥平 面
面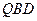 ;
;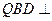 平面
平面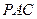
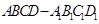 中,
中,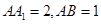 ,点
,点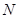 是
是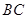 的中点,点
的中点,点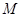 在
在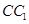 上,设二面角
上,设二面角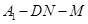 的大小为
的大小为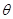 。
。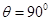 时,求
时,求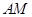 的长;
的长;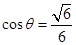 时,求
时,求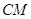 的长。
的长。