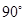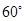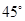题目内容
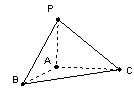
如图,平面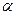 ⊥平面
⊥平面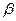 ,
,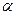 ∩
∩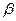 =
=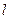 ,DA
,DA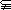
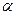 ,BC
,BC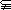
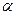 ,且DA⊥
,且DA⊥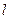 于A,BC⊥
于A,BC⊥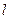 于B,AD=4,BC=8,AB=6,在平面
于B,AD=4,BC=8,AB=6,在平面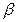 内不在
内不在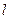 上的动点P,记PD与平面
上的动点P,记PD与平面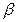 所成角为
所成角为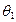 ,PC与平面
,PC与平面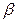 所成角为
所成角为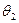 ,若
,若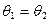 ,则△PAB的面积的最大值是 。
,则△PAB的面积的最大值是 。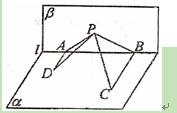
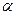 ⊥平面
⊥平面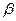 ,
,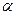 ∩
∩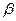 =
=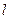 ,DA
,DA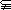
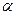 ,BC
,BC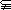
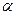 ,且DA⊥
,且DA⊥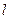 于A,BC⊥
于A,BC⊥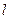 于B,AD=4,BC=8,AB=6,在平面
于B,AD=4,BC=8,AB=6,在平面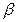 内不在
内不在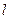 上的动点P,记PD与平面
上的动点P,记PD与平面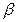 所成角为
所成角为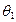 ,PC与平面
,PC与平面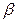 所成角为
所成角为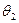 ,若
,若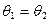 ,则△PAB的面积的最大值是 。
,则△PAB的面积的最大值是 。
12
由条件可得:PB=2PA,即P到B的距离为到A的距离的2倍
在平面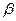 内以AB为
内以AB为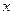 轴,AB的中垂线为
轴,AB的中垂线为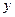 轴,建立平面直角坐标系
轴,建立平面直角坐标系
设P(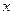 ,
,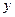 )则
)则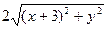 =
=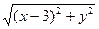
∴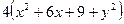 =
=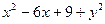 ∴
∴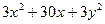 +27=0
+27=0
∴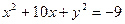 ∴
∴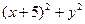 =16
=16
∴平面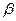 内P点轨迹为以(
内P点轨迹为以(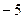 ,0)为圆心,4为半径的圆(与
,0)为圆心,4为半径的圆(与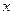 轴的交点除外)
轴的交点除外)
∴高的最大值为4, ∴面积的最大值为 =12
=12
在平面
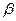 内以AB为
内以AB为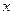 轴,AB的中垂线为
轴,AB的中垂线为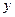 轴,建立平面直角坐标系
轴,建立平面直角坐标系设P(
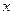 ,
,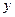 )则
)则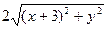 =
=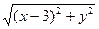
∴
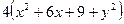 =
=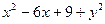 ∴
∴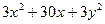 +27=0
+27=0∴
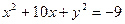 ∴
∴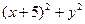 =16
=16∴平面
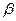 内P点轨迹为以(
内P点轨迹为以(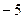 ,0)为圆心,4为半径的圆(与
,0)为圆心,4为半径的圆(与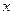 轴的交点除外)
轴的交点除外)∴高的最大值为4, ∴面积的最大值为
 =12
=12
练习册系列答案
相关题目
 知四棱锥
知四棱锥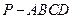 的底面为直角梯形,AD∥BC,∠BCD=90°
的底面为直角梯形,AD∥BC,∠BCD=90° ,PA=PB,PC=PD
,PA=PB,PC=PD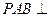 平面ABCD;
平面ABCD;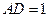
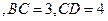 ,且侧面
,且侧面 的面积为8,求四棱锥
的面积为8,求四棱锥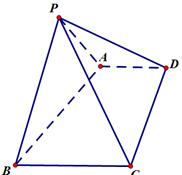
 ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。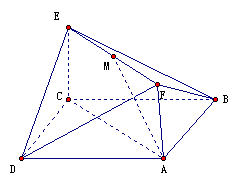
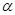 与平面
与平面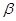 相交,直线
相交,直线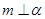 ,则( )
,则( )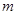 平行,且存在直线与
平行,且存在直线与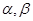 是两个不同的平面,m,n是两条不同的直线,给出下列命题:
是两个不同的平面,m,n是两条不同的直线,给出下列命题: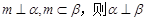 ; ②若
; ②若 ;
;  相交;
相交; 其中正确的命题是 ( )
其中正确的命题是 ( ) 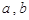 为直线,
为直线,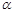 为平面):
为平面):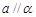 ,
,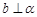 ,则
,则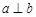 ;
;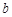 有且只有一个平面与
有且只有一个平面与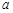 垂直.
垂直.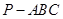 中,
中,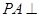 平面
平面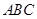 ,
,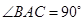 ,
,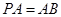 ,则直线
,则直线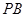 与平面
与平面