题目内容
 如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,
如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,(1)求证:AB⊥面BCD;
(2)求点C到面ABD的距离.
分析:(1)由AB=BC=a,∠C=135°,知∠BCA=45°,∠ACD=90°,DC⊥AC,由题知沿对角AC将四边形折成直二面角,从而得到DC⊥平面ABC,DC⊥AB,再由∠B=90°,能够证明AB⊥平面BCD.
(2)过点C作CE⊥BD,由(1)可知,CE⊥AB,从而得到CE⊥平面ABD,CE的长度为点C到平面ABD的距离,由此能求出点C到面ABD的距离.
(2)过点C作CE⊥BD,由(1)可知,CE⊥AB,从而得到CE⊥平面ABD,CE的长度为点C到平面ABD的距离,由此能求出点C到面ABD的距离.
解答:(1)证明:因为AB=BC=a,∠C=135°,
所以∠BCA=45°,∠ACD=90°,所以DC⊥AC,
由题知沿对角AC将四边形折成直二面角,
所以 DC⊥平面ABC,所以DC⊥AB,
而∠B=90°,所以AB⊥BC,
故AB⊥平面BCD.
(2)解:过点C作CE⊥BD,
由(1)可知,CE⊥AB,所以CE⊥平面ABD,
∴CE的长度为点C到平面ABD的距离,
∵BC=CD=a,DC⊥BC,
∴DE=
.
故点C到面ABD的距离为
.
所以∠BCA=45°,∠ACD=90°,所以DC⊥AC,
由题知沿对角AC将四边形折成直二面角,
所以 DC⊥平面ABC,所以DC⊥AB,
而∠B=90°,所以AB⊥BC,
故AB⊥平面BCD.
(2)解:过点C作CE⊥BD,
由(1)可知,CE⊥AB,所以CE⊥平面ABD,
∴CE的长度为点C到平面ABD的距离,
∵BC=CD=a,DC⊥BC,
∴DE=
| ||
| 2 |
故点C到面ABD的距离为
| ||
| 2 |
点评:本题考查直线与平面垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
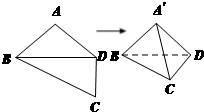 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD=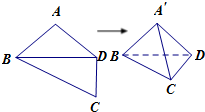 如图,平面四边形ABCD中,AB=AD=CD=1,
如图,平面四边形ABCD中,AB=AD=CD=1, 如图,平面四边形ABCD中,AB=13,AC=10,AD=5,
如图,平面四边形ABCD中,AB=13,AC=10,AD=5,