题目内容
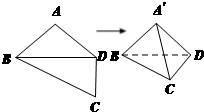 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
分析:由题意可知,四面体A'-BCD顶点在同一个球面上,BC的中点就是球心,求出球的半径,即可得到球的体积.
解答:解:平面四边形ABCD中,AB=AD=CD=1,BD=
,BD⊥CD,将其沿对角线BD折成四面体A'-BCD,
使平面A'BD⊥平面BCD.四面体A'-BCD顶点在同一个球面上,△BCD和△A'BC都是直角三角形,
BC的中点就是球心,所以BC=
,球的半径为:
;
所以球的体积为:
×(
)3=
π;
故答案为:
π.
| 2 |
使平面A'BD⊥平面BCD.四面体A'-BCD顶点在同一个球面上,△BCD和△A'BC都是直角三角形,
BC的中点就是球心,所以BC=
| 3 |
| ||
| 2 |
所以球的体积为:
| 4π |
| 3 |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题是基础题,考查四面体的外接球的体积的求法,找出外接球的球心,是解题的关键,考查计算能力,空间想象能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
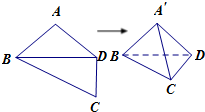 如图,平面四边形ABCD中,AB=AD=CD=1,
如图,平面四边形ABCD中,AB=AD=CD=1, 如图,平面四边形ABCD中,AB=13,AC=10,AD=5,
如图,平面四边形ABCD中,AB=13,AC=10,AD=5, 如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,
如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,