题目内容
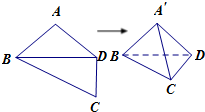 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
A、
| ||||
| B、3π | ||||
C、
| ||||
| D、2π |
分析:说明折叠后几何体的特征,求出三棱锥的外接球的半径,然后求出球的体积.
解答:解:由题意平面四边形ABCD中,AB=AD=CD=1,BD=
,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,可知A′B⊥A′C,所以BC 是外接球的直径,所以BC=
,球的半径为:
;所以球的体积为:
(
)3=
π.
故选A
| 2 |
| 3 |
| ||
| 2 |
| 4π |
| 3 |
| ||
| 2 |
| ||
| 2 |
故选A
点评:本题是基础题,考查折叠问题,三棱锥的外接球的体积的求法,考查计算能力,正确球的外接球的半径是解题的关键.

练习册系列答案
相关题目
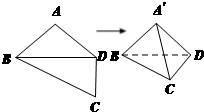 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD= 如图,平面四边形ABCD中,AB=13,AC=10,AD=5,
如图,平面四边形ABCD中,AB=13,AC=10,AD=5, 如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,
如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,