题目内容

如图，平面四边形ABCD中，AB=13，AC=10，AD=5，cos∠DAC=
3
5
，
AB
•
AC
=120．
（1）求cos∠BAD；
（2）设
AC
=x•
AB
+y•
AD
，求x、y的值．
分析：（1）设∠CAB=α，∠CAD=β，由AB=13，AC=10，
AB
•
AC
=120．可得α的余弦值，又由cos∠DAC=
3
5
，分别求出两个角的正弦值，代入两角和的余弦公式，可得答案．
（2）若
AC
=x•
AB
+y•
AD
，则
AC
•
AB
=x
AB
2+y
AD
•
AB
AC
•
AD
=x
AB
•
AD
+y
AD
2
，结合AD=5，及（1）中结论，可得x、y值．
解答：解：（1）设∠CAB=α，∠CAD=β，
cosα=
AB
•
AC
|
AB
|•|
AC
|
=
120
130
=
12
13
，cosβ=
3
5
，
∴sinα=
5
13
，sinβ=
4
5
，…．（3分）
∴cos∠BAD=cos（α+β）=cosαcosβ-sinαsinβ=
12
13
•
3
5
-
5
13
•
4
5
=
16
65
…..（6分）
（2）由
AC
=x•
AB
+y•
AD
得：
AC
•
AB
=x
AB
2+y
AD
•
AB
AC
•
AD
=x
AB
•
AD
+y
AD
2
…．（8分）
∴
120=169x+16y
30=16x+25y
…..（10分）
解得：x=
40
63
，y=
50
63
．  …（12分）
点评：本题考查的知识点是平面向量的数量积运算，熟练掌握平面向量夹角公式及数量积公式是解答的关键．
练习册系列答案
相关题目
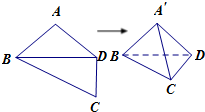精英家教网如图，平面四边形ABCD中，AB=AD=CD=1，BD=
2
，BD⊥CD，将其沿对角线BD折成四面体A′-BCD，使平面A′BD⊥平面BCD．四面体A′-BCD顶点在同一个球面上，则该球的体积为
 
．
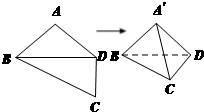
精英家教网如图，平面四边形ABCD中，AB=AD=CD=1，BD=
2
，BD⊥CD，将其沿对角线BD折成四面体A′-BCD，使平面A′BD⊥平面BCD，若四面体A′-BCD顶点在同一个球面上，则该球的体积为（　　）
A、
3
2
π
B、3π
C、
2
3
π
D、2π
如图：平面四边形ABCD中，AB=BC=CD=a，∠B=90°，∠BCD=135°，沿对角线AC将△ADC折起，使面ADC⊥面ABC，
（1）求证：AB⊥面BCD；
（2）求点C到面ABD的距离．
在如图的平面四边形中，AB=80，∠ABC=105°，∠BAC=30°，∠BAD=90°∠ABD=45°，求DC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网