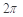题目内容
在如图的平面四边形中,AB=80,∠ABC=105°,∠BAC=30°,∠BAD=90°∠ABD=45°,求DC的长.

分析:利用△DAB是等腰直角三角形,AB=80,可求的BD,进而可求BC,由此利用余弦定理,可求得DC长.
解答:解:由题意,∵∠BAD=90°,∠ABD=45°
∴△DAB是等腰直角三角形,
∵AB=80,
∴BD=80
…(4分)
在△ABC中,∵∠ABC=105°,∠BAC=30°
∴∠ACB=45°,
∵∠BAC=30°,
由正弦定理:
=
∴BC=40
…(4分)
∵在△BDC中,∠DBC=60°,BD=80
,
由余弦定理:DC2=BD2+BC2-2DC•BCcos60°=9600,
∴DC=40
…(4分)
∴△DAB是等腰直角三角形,
∵AB=80,
∴BD=80
| 2 |
在△ABC中,∵∠ABC=105°,∠BAC=30°
∴∠ACB=45°,
∵∠BAC=30°,
由正弦定理:
| 80 |
| sin45° |
| BC |
| sin30° |
∴BC=40
| 2 |
∵在△BDC中,∠DBC=60°,BD=80
| 2 |
由余弦定理:DC2=BD2+BC2-2DC•BCcos60°=9600,
∴DC=40
| 6 |
点评:本题以平面图形为载体,考查正弦定理,余弦定理,属于基础题.

练习册系列答案
相关题目
 中,
中,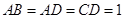 ,
,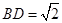 ,
,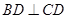 ,将其沿对角线
,将其沿对角线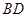 折成四面体
折成四面体 ,使平面
,使平面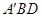
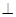 平面
平面 ,若四面体
,若四面体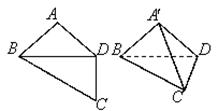
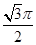 B.
B.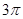 C.
C. 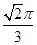 D.
D.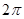
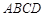 中,
中,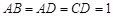 ,
,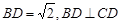 ,将其沿对角线
,将其沿对角线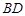 折成四面体
折成四面体 ,使平面
,使平面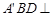 平面
平面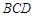 ,若四面体
,若四面体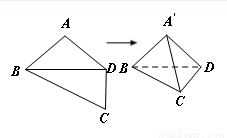
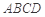 中,
中,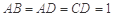 ,
,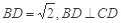 ,将其沿对角线
,将其沿对角线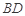 折成四面体
折成四面体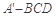 ,使平面
,使平面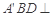 平面
平面 ,若四面体
,若四面体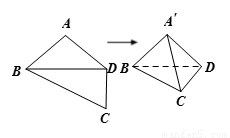
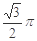 B.
B.
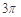
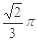 D.
D.