题目内容
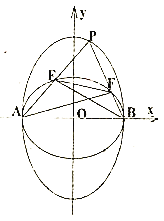
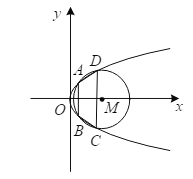
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 在第一象限的交点为
在第一象限的交点为![]() ,椭圆
,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其中
,其中![]() 也是抛物线
也是抛物线![]() 的焦点,且
的焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左顶点,直线
的左顶点,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意,由抛物线性质可求焦点坐标和![]() 点坐标,结合椭圆定义,可求
点坐标,结合椭圆定义,可求![]() ,计算即可求解;
,计算即可求解;
(2)设![]() ,讨论直线
,讨论直线![]() 与
与![]() 轴是否垂直,再根据直线与椭圆方程联立方程组法,结合韦达定理,计算
轴是否垂直,再根据直线与椭圆方程联立方程组法,结合韦达定理,计算![]() ,即可证明.
,即可证明.
(1)抛物线![]() 的焦点为
的焦点为![]() ,
,
![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程是:
的方程是:![]() ;
;
(2)设![]()
当直线![]() 与
与![]() 轴垂直时,易得:
轴垂直时,易得:![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() ,或者
,或者![]() ,
,
∴![]() ,∴
,∴![]()
当直线![]() 与
与![]() 不垂直时,设直线
不垂直时,设直线![]() 的方程为:
的方程为:![]() ,
,
联方程组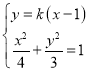 ,消去
,消去![]() 整理得:
整理得:![]() ,
,
所以:![]() ,
,
又![]() 共线,
共线,
∴![]() ,得
,得![]() ,同理:
,同理:![]() ,
,
∴![]() ,
,
∴![]()
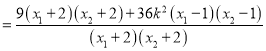
又因为![]()
![]()
![]()
∴![]() ,则
,则![]()
综上,![]() 为定值.
为定值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分别五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意),其统计结果如下表(住宿满意度为x,餐饮满意度为y).
餐饮满意度y 人数 住宿满意度x | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 2 | 1 | 0 |
2 | 2 | 1 | 3 | 2 | 1 |
3 | 1 | 2 | 5 | 3 | 4 |
4 | 0 | 3 | 5 | 4 | 3 |
5 | 0 | 0 | 1 | 2 | 3 |
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.