题目内容
已知数列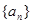 的前
的前 项和
项和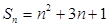 ,则通项
,则通项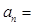
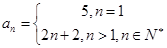
解析

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
设 是等差数列
是等差数列 的前
的前 项和,公差
项和,公差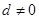 ,若
,若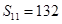 ,若
,若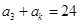 ,则正整数
,则正整数 的值为( )
的值为( )
A.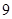 | B.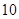 | C. | D.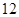 |
题目内容
已知数列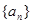 的前
的前 项和
项和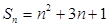 ,则通项
,则通项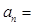
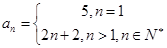
解析

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案设 是等差数列
是等差数列 的前
的前 项和,公差
项和,公差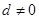 ,若
,若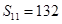 ,若
,若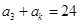 ,则正整数
,则正整数 的值为( )
的值为( )
A.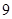 | B.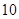 | C. | D.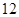 |