题目内容
已知数列{an}中,a1=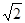 ,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+
,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+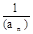 (
(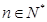 ),数列{bn}中,b1=1,b2=2,
),数列{bn}中,b1=1,b2=2,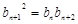 (
(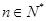 ),则a1b1+ a2b2+…+anbn=
),则a1b1+ a2b2+…+anbn=
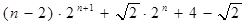
解析试题分析: 因为数列{an}中,a1=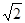 ,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+
,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+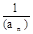 (
(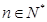 ),则可知a2=
),则可知a2=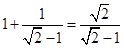 ,依次可得
,依次可得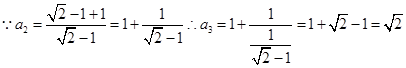 ,还可得数列的周期性为2,数列{bn}中,b1=1,b2=2,
,还可得数列的周期性为2,数列{bn}中,b1=1,b2=2,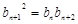 (
(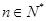 ),因此可知数列{bn}是等比数列,公比为2,故bn=2n-1,因此利用分组求和可知
),因此可知数列{bn}是等比数列,公比为2,故bn=2n-1,因此利用分组求和可知
a1b1+ a2b2+…+anbn=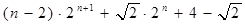 ,故答案为
,故答案为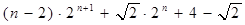 。
。
考点:本题主要考查了数列的通项公式和前n项和的求解的运用。
点评:解决该试题的关键是对于两个数列通项公式的分析和求解,然后能合理的选用求公式来得到结论。

练习册系列答案
相关题目
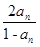 ,则a5= .
,则a5= .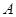 和一个运算出口
和一个运算出口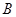 ,执行某种运算程序.
,执行某种运算程序.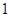 时,从
时,从 ,记为
,记为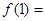
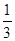 ;
;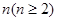 时,在
时,在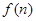 是前一结果
是前一结果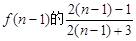 倍.
倍.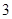 时,从
时,从 ,则应从
,则应从 ,数列
,数列 满足
满足 ,且数列
,且数列 的取值范围是
的取值范围是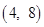
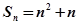 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________ 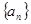 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足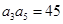 ,
, 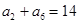 .
. 的通项公式;
的通项公式; 满足:
满足: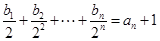
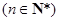 ,求数列
,求数列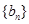 的前
的前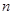 项和.
项和.
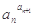 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )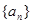 的前
的前 项和
项和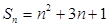 ,则通项
,则通项