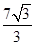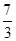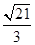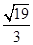题目内容
(5分)(2011•广东)设圆C与圆x2+(y﹣3)2=1外切,与直线y=0相切,则C的圆心轨迹为( )
| A.抛物线 | B.双曲线 | C.椭圆 | D.圆 |
A
解析试题分析:由动圆与定圆相外切可得两圆圆心距与半径的关系,然后利用圆与直线相切可得圆心到直线的距离与半径的关系,借助等量关系可得动点满足的条件,即可的动点的轨迹.
解:设C的坐标为(x,y),圆C的半径为r,圆x2+(y﹣3)2=1的圆心为A,
∵圆C与圆x2+(y﹣3)2=1外切,与直线y=0相切∴|CA|=r+1,C到直线y=0的距离d=r
∴|CA|=d+1,即动点C定点A的距离等于到定直线y=﹣1的距离
由抛物线的定义知:C的轨迹为抛物线.
故选A
点评:本题考查了圆的切线,两圆的位置关系及抛物线的定义,动点的轨迹的求法,是个基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
椭圆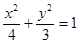 的焦点坐标为( )
的焦点坐标为( )
A.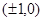 | B.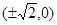 | C.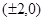 | D.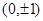 |
若抛物线 的焦点与椭圆
的焦点与椭圆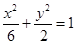 的左焦点重合,则
的左焦点重合,则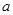 的值为( )
的值为( )
| A.-8 | B.-16 | C.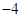 | D.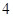 |
设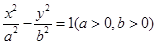 的离心率为
的离心率为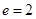 ,则
,则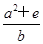 的最小值为( )
的最小值为( )
A.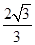 | B.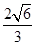 | C.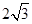 | D.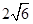 |
直线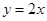 为双曲线
为双曲线 的一条渐近线,则双曲线
的一条渐近线,则双曲线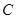 的离心率是( )
的离心率是( )
A. | B. | C.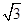 | D.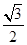 |
已知双曲线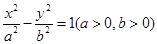 的一条渐近线平行于直线
的一条渐近线平行于直线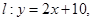 双曲线的一个焦点在直线
双曲线的一个焦点在直线 上,则双曲线的方程为( )
上,则双曲线的方程为( )
A.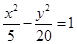 | B.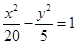 | C.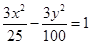 | D.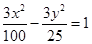 |
(2011•浙江)已知椭圆C1: =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣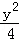 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
A.a2=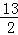 | B.a2=3 | C.b2= | D.b2=2 |
已知椭圆C的方程为 (m>0),如果直线y=
(m>0),如果直线y=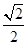 x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
| A.2 | B.2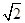 |
| C.8 | D.2 |
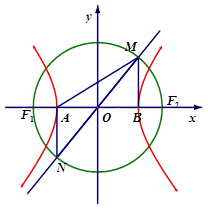
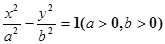 的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足
的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足 MAN=120o,则该双曲线的离心率为( )
MAN=120o,则该双曲线的离心率为( )