题目内容
已知二次函数f(x)的图象顶点为A(1,16),且图象在x轴上截得线段长为8.
(1)求函数f(x)的解析式;
(2)当x∈[0,2]时,关于x的函数g(x)=f(x)-(t-x)x-3的图象始终在x轴上方,求实数t的取值范围.
(1)求函数f(x)的解析式;
(2)当x∈[0,2]时,关于x的函数g(x)=f(x)-(t-x)x-3的图象始终在x轴上方,求实数t的取值范围.
(1)∵二次函数图象顶点为(1,16),
∴函数的对称轴为x=1
∵在x轴上截得线段长为8,
∴抛物线与x轴的交点坐标为(-3,0),(5,0),…(2分)
又∵开口向下,设原函数为f(x)=a(x+3)(x-5)(a<0)…(4分)
将(1,16)代入得a=-1,…(6分)
∴所求函数f(x)的解析式为f(x)=-x2+2x+15.…(7分)
(2)g(x)=f(x)-(t-x)x-3=(2-t)x+12,x∈[0,2]…(9分)
由g(x)得图象在x轴上方,根据一次函数的性质可得
,…(12分)
即-2t+16>0
解得t<8…(14分)
∴函数的对称轴为x=1
∵在x轴上截得线段长为8,
∴抛物线与x轴的交点坐标为(-3,0),(5,0),…(2分)
又∵开口向下,设原函数为f(x)=a(x+3)(x-5)(a<0)…(4分)
将(1,16)代入得a=-1,…(6分)
∴所求函数f(x)的解析式为f(x)=-x2+2x+15.…(7分)
(2)g(x)=f(x)-(t-x)x-3=(2-t)x+12,x∈[0,2]…(9分)
由g(x)得图象在x轴上方,根据一次函数的性质可得
|
即-2t+16>0
解得t<8…(14分)

练习册系列答案
相关题目


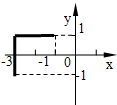
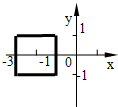
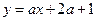 ,当
,当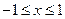 时,
时,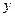 的值有正有负,则实数
的值有正有负,则实数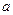 的范围 .
的范围 . 