题目内容
若函数f(x)的定义域是[0,4],则函g(x)=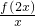 的定义域是
的定义域是
- A.[0,2]
- B.(0,2)
- C.(0,2]
- D.[0,2)
C
分析:根据f(2x)中的2x和f(x)中的x的取值范围一样得到:0≤2x≤4,又分式中分母不能是0,即:x≠0,解出x的取值范围,得到答案.
解答:因为f(x)的定义域为[0,4],
所以对g(x),0≤2x≤4但x≠0故x∈(0,1],
故选C.
点评:本题考查求复合函数的定义域问题,解决此类题目的关键是f[g(x)]中g(x)相当于f(x)中的x,建立不等式,属中档题.
分析:根据f(2x)中的2x和f(x)中的x的取值范围一样得到:0≤2x≤4,又分式中分母不能是0,即:x≠0,解出x的取值范围,得到答案.
解答:因为f(x)的定义域为[0,4],
所以对g(x),0≤2x≤4但x≠0故x∈(0,1],
故选C.
点评:本题考查求复合函数的定义域问题,解决此类题目的关键是f[g(x)]中g(x)相当于f(x)中的x,建立不等式,属中档题.

练习册系列答案
相关题目