题目内容
【题目】下列命题中，假命题为( )
A. 存在四边相等的四边形不是正方形
B. z1，z2∈C，z1＋z2为实数的充分必要条件是z1，z2互为共轭复数
C. 若x，y∈R，且x＋y>2，则x，y至少有一个大于1
D. 对于任意n∈N＋，
都是偶数
【答案】B
【解析】
举空间四边形可得A为真，举反例可得B为假，利用反证法可得C为真，根据二项式系数性质可得D为真.
空间四边形可能四边相等，但不是正方形，故A为真命题；令z1＝1＋bi，z2＝3－bi(b∈R)，显然z1＋z2＝4∈R，但z1，z2不互为共轭复数，B为假命题；假设x，y都不大于1，则x＋y>2不成立，故与题设条件“x＋y>2”矛盾，假设不成立，故C为真命题；C
＋C
＋…＋C
＝2n为偶数，故D为真命题．排除A，C，D，应选B.
【题目】随着网络时代的进步，流量成为手机的附带品，人们可以利用手机随时随地的浏览网页，聊天，看视频，因此，社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查，所得结果统计如下图所示：
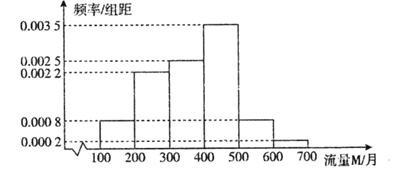
（Ⅰ)以频率估计概率，若在该地区任取3位居民，其中恰有
位居民的月流量的使用情况
在300M∽400M之间，求
的期望
；
（Ⅱ）求被抽查的居民使用流量的平均值；
（Ⅲ）经过数据分析，在一定的范围内，流量套餐的打折情况
与其日销售份数
成线性相关
关系，该研究人员将流量套餐的打折情况
与其日销售份数
的结果统计如下表所示：
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立
关于
的的回归方程.
附注：回归方程
中斜率和截距的最小二乘估计公式分别为：
， 
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
.
， 
(1)求
， 
；
(2)若 与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？
