题目内容
15.已知loga3.14>logaπ,则实数a的取值范围是(0,1).分析 讨论底数与1的关系,确定函数的单调性,根据函数的单调性整理出关于a的不等式,得到结果,把两种情况求并集得到结果.
解答 解:当a>1时,函数是一个增函数,不等式的解是3,14>π不成立,
当0<a<1时,函数是一个减函数,不等式的解是3.14<π成立,
综上可知:0<a<1.
故答案为:(0,1).
点评 本题主要考查对数函数单调性的应用、不等式的解法等基础知识,本题解题的关键是对于底数与1的关系,这里应用分类讨论思想来解题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
10.对于任意两个事件A,B,有P(A-B)为( )
| A. | P(A)-P(B) | B. | P(A)+P($\overline{B}$)-P(A$\overline{B}$) | C. | P(A)-P(AB) | D. | P(A)-P(B)+P(AB) |
20.已知单位向量$\overrightarrow{e}$与向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$-$\overrightarrow{e}$|=|$\overrightarrow{a}$|,($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{b}$-$\overrightarrow{e}$)=0,对每一个确定的向量$\overrightarrow{a}$,都有与其对应的向量$\overrightarrow{b}$满足以上条件,设M,m分别为|$\overrightarrow{b}$|的最大值和最小值,令t=M-m,则对任意的向量$\overrightarrow{a}$,实数t的取值范围是 ( )
| A. | [0,1] | B. | [0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
4.已知复数z1=3+2i,z2=1-2i,则复数z=z1-z2在复平面内对应点Z位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
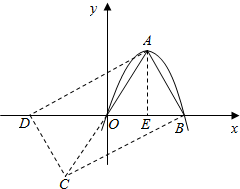 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.