题目内容
理在直角坐标平面内,已知三点A、B、C共线,函数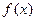 满足:
满足: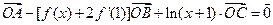 (1)求函数
(1)求函数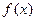 的表达式;(2)若
的表达式;(2)若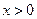 ,求证:
,求证: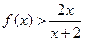 ;(3)若不等式
;(3)若不等式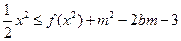 对任意
对任意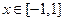 及任意
及任意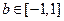 都成立,求实数
都成立,求实数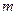 的取值范围。
的取值范围。
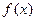 满足:
满足: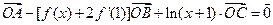 (1)求函数
(1)求函数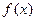 的表达式;(2)若
的表达式;(2)若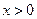 ,求证:
,求证: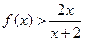 ;(3)若不等式
;(3)若不等式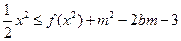 对任意
对任意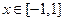 及任意
及任意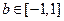 都成立,求实数
都成立,求实数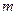 的取值范围。
的取值范围。(1)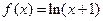 (2)略(3)
(2)略(3)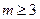 或
或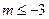
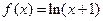 (2)略(3)
(2)略(3)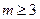 或
或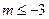
(1)∵三点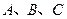 共线且
共线且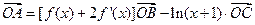
∴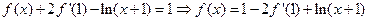
由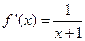 得
得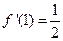 故
故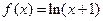 ………4分
………4分
(2)证明:记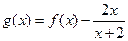 则
则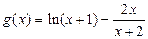
∵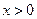 时
时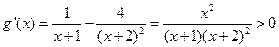
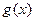 在
在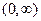 上是单调增函数故
上是单调增函数故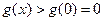 即
即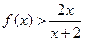 成立………9分
成立………9分
(3)记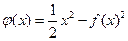 则
则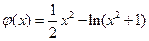
由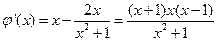 又
又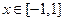 知
知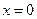 时
时
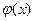 取的最大值,且
取的最大值,且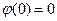 故原命题可化为对任意
故原命题可化为对任意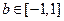 都有:
都有:
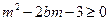 恒成立记
恒成立记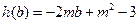 知
知 时
时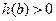 恒成立
恒成立
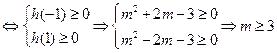 或
或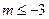 ………14分
………14分
 共线且
共线且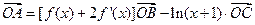
∴
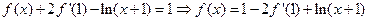
由
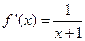 得
得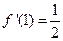 故
故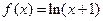 ………4分
………4分(2)证明:记
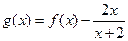 则
则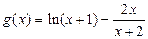
∵
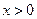 时
时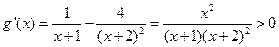
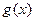 在
在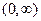 上是单调增函数故
上是单调增函数故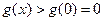 即
即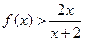 成立………9分
成立………9分(3)记
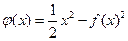 则
则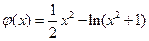
由
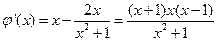 又
又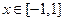 知
知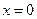 时
时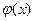 取的最大值,且
取的最大值,且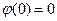 故原命题可化为对任意
故原命题可化为对任意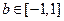 都有:
都有: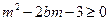 恒成立记
恒成立记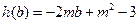 知
知 时
时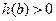 恒成立
恒成立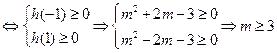 或
或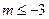 ………14分
………14分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
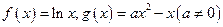 .
.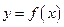 与
与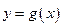 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数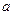 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数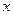 轴的垂线分别与
轴的垂线分别与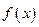 的图像和
的图像和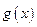 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作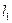 ,以T为切点作
,以T为切点作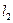 .是否存在实数
.是否存在实数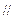
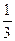 时, 函数取得极大值, 则m的值为 ( )
时, 函数取得极大值, 则m的值为 ( )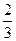
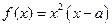 .
.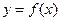 在点
在点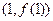 处的切线
处的切线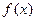 在区间[0,2]上的最大值。
在区间[0,2]上的最大值。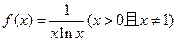
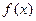 的单调区间;
的单调区间;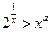 对任意
对任意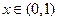 成立,求实数
成立,求实数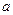 的取值范围。
的取值范围。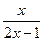 在点(1,1)处的切线方程为( )
在点(1,1)处的切线方程为( )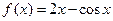 在
在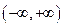 上( )
上( )
 ,
, ( )
( )


