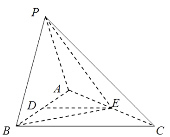
题目内容
【题目】在![]() 中,边
中,边![]() ,
,![]() 所在直线的方程分别为
所在直线的方程分别为![]() ,
,![]() ,已知
,已知![]() 是
是![]() 边上一点.
边上一点.
(1)若![]() 为
为![]() 边上的高,求直线
边上的高,求直线![]() 的方程;
的方程;
(2)若![]() 为
为![]() 边的中线,求
边的中线,求![]() 的面积.
的面积.
【答案】(1)![]() (2)6
(2)6
【解析】试题分析:
(1)利用题意首先求得BC的斜率,然后由点斜式可得直线![]() 的方程为
的方程为![]() ;
;
(2)由题意可得三角形的高为![]() ,结合几何关系可得
,结合几何关系可得![]() 的面积为6.
的面积为6.
试题解析:
(1)由![]() 解得
解得![]() ,即
,即![]() ,分
,分
又![]() ,所以
,所以![]() ,
,
因为![]() 为
为![]() 边上的高,所以
边上的高,所以![]() ,
,
![]() 为
为![]() 边上一点,所以
边上一点,所以![]()
![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)法一:设点![]() 的坐标为
的坐标为![]() ,由
,由![]() 为
为![]() 的中点,得点
的中点,得点![]() 的坐标为
的坐标为![]() ,
,
又点![]() 与点
与点![]() 分别在直线
分别在直线![]() 和
和![]() 上,
上,
所以![]() ,解得
,解得![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
由(1)得![]() ,又
,又![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
又![]() ,
,
所以![]() ,
,
又![]() 为
为![]() 的中点
的中点
所以![]() .
.
法二:(上同法一)
点![]() 的坐标为
的坐标为![]() ,
,
又![]() 为
为![]() 上一点,
上一点,
所以直线![]() 的方程为
的方程为![]() .
.
由(1)知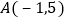 ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离
![]() ,
,
又![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,
所以![]() .
.
法三:若直线![]() 的斜率不存在,即
的斜率不存在,即![]() 的方程为
的方程为![]() ,
,
由![]() 解得
解得![]() ,
,
即![]() 的坐标为
的坐标为![]() ,同理可得
,同理可得![]() 的坐标为
的坐标为![]() ,
,
而![]() ,
, ![]() 不是
不是![]() 的中点,所以直线
的中点,所以直线![]() 的斜率存在.
的斜率存在.
设直线![]() 的方程为
的方程为![]()
由![]() 解得
解得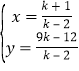 ,即
,即![]() 的坐标为
的坐标为![]() 同理可得
同理可得![]() 的坐标为
的坐标为![]() ,
,![]() 为
为![]() 的中点
的中点
所以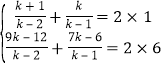 解得
解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即为
,即为![]() .
.
(下同法二)
法四:求![]() 正弦值即
正弦值即![]() ,
,![]() 长用面积公式(略).
长用面积公式(略).

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: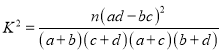 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |