��Ŀ����
�ڵȲ�����{an}�У�a1=3����ǰn���ΪSn���ȱ�����{bn}�ĸ����Ϊ������b1=1������Ϊq,��b2+ S2=12��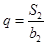 .������an ��bn������������{cn}����
.������an ��bn������������{cn}����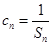 ����{cn}��ǰn���Tn.
����{cn}��ǰn���Tn.
����������������Ҫ�ǿ����˵ȱ����е�ͨ�ʽ����͵����á���һ���У����õȱ�����{bn}�ĸ����Ϊ������b1=1������Ϊq,��b2+ S2=12��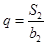 ���ɵ�
���ɵ�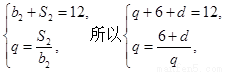 �����q=3��q=-4(��),d=3.�õ�ͨ�ʽ��an=3+3(n-1)=3n, bn=3 n-1. �ڶ����У�
�����q=3��q=-4(��),d=3.�õ�ͨ�ʽ��an=3+3(n-1)=3n, bn=3 n-1. �ڶ����У�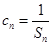 ���ɵ�һ����֪��
���ɵ�һ����֪�� ��Ȼ������������͵õ�Tn.
��Ȼ������������͵õ�Tn.
�⣺ (��) �裺{an}�Ĺ���Ϊd,
��Ϊ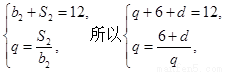 ���q=3��q=-4(��),d=3.
���q=3��q=-4(��),d=3.
��an=3+3(n-1)=3n, bn=3 n-1. ������6��
(��)��Ϊ ����������8��
����������8��
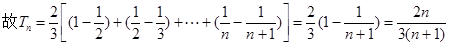
���𰸡�
(��) an=3+3(n-1)=3n, bn=3
n-1. (�� 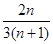

��ϰ��ϵ�д�
�����Ŀ