题目内容
(2013•临沂一模)已知等比数列{an}的首项为l,公比q≠1,Sn为其前n项和,al,a2,a3分别为某等差数列的第一、第二、第四项.
(I)求an和Sn;
(Ⅱ)设bn=log2an+1,数列{
}的前n项和为Tn,求证:Tn<
.
(I)求an和Sn;
(Ⅱ)设bn=log2an+1,数列{
| 1 |
| bnbn+2 |
| 3 |
| 4 |
分析:(I)由题意可得a3-a2=2(a2-a1),结合等比数列的通项公式表示已知,解方程可求q,进而利用等比数列的通项公式可求通项及和
(II)由(I)可知,bn=log2an+1=n,代入
=
=
(
-
),利用裂项求和方法即可求解Tn,可证明
(II)由(I)可知,bn=log2an+1=n,代入
| 1 |
| bnbn+2 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
解答:解:(I)al,a2,a3分别为某等差数列的第一、第二、第四项
∴a3-a2=2(a2-a1)
∴a1q2-a1q=2a1q-2a1
∵a1=1
∴q2-3q+2=0
∴q=2
∴an=2n-1
sn=
=2n-1
(II)由(I)可知,bn=log2an+1=n
∴
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)
=
(1+
-
-
)
=
-
(
+
)<
∴a3-a2=2(a2-a1)
∴a1q2-a1q=2a1q-2a1
∵a1=1
∴q2-3q+2=0
∴q=2
∴an=2n-1
sn=
| 1-2n |
| 1-2 |
(II)由(I)可知,bn=log2an+1=n
∴
| 1 |
| bnbn+2 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
点评:本题主要考查了等差数列的性质及等比数列的通项公式的应用,数列的裂项求和方法的应用

练习册系列答案
相关题目
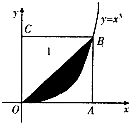 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )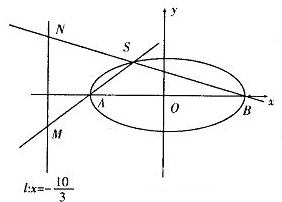 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: