题目内容
(2013•临沂一模)定义在R上的偶函数f(x)对任意的x∈R有f(1+x)=f(1-x),且当x∈[2,3]时,f(x)=-x2+6x-9.若函数y=f(x)-logax在(0,+∞)上有四个零点,则a的值为
.
| 1 |
| 4 |
| 1 |
| 4 |
分析:由已知中f(x+1)=f(1-x),故可能函数是以2为周期的周期函数,又由函数f(x)是定义在R上的偶函数,结合当x∈[2,3]时,f(x)=-x2+6x-9.我们易得函数f(x)的图象,最后利用图象研究零点问题即可.
解答: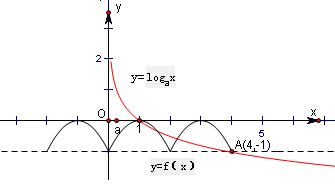 解:由函数f(x)是定义在R上的偶函数,且f(x+1)=f(1-x)成立,
解:由函数f(x)是定义在R上的偶函数,且f(x+1)=f(1-x)成立,
可得f(x+2)=f(-x)=f(x),
∴函数f(x)是定义在R上的周期为2的偶函数,
当x∈[2,3]时,f(x)=-x2+6x-9.
函数y=f(x)-logax在(0,+∞)上的零点个数等于函数y=f(x)和函数y=logax的图象在(0,+∞)上的交点个数,如图所示:
当y=logax的图象过点A(4,-1)时,函数y=f(x)-logax在(0,+∞)上有四个零点,
∴-1=loga4,∴a=
.
故答案为:
.
 解:由函数f(x)是定义在R上的偶函数,且f(x+1)=f(1-x)成立,
解:由函数f(x)是定义在R上的偶函数,且f(x+1)=f(1-x)成立,可得f(x+2)=f(-x)=f(x),
∴函数f(x)是定义在R上的周期为2的偶函数,
当x∈[2,3]时,f(x)=-x2+6x-9.
函数y=f(x)-logax在(0,+∞)上的零点个数等于函数y=f(x)和函数y=logax的图象在(0,+∞)上的交点个数,如图所示:
当y=logax的图象过点A(4,-1)时,函数y=f(x)-logax在(0,+∞)上有四个零点,
∴-1=loga4,∴a=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查的知识点是函数奇偶性与单调性的综合应用,函数的周期性,考查函数的零点与方程的根的关系,体现了化归与转化与数形结合的数学思想,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
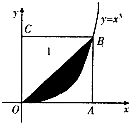 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )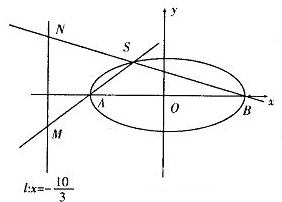 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: