题目内容
（2013•临沂一模）函数f(x)=ln
+x
的定义域为（ ）
| x |
| x-1 |
| 1 |
| 2 |
分析：由对数式的真数大于0，无理式根号内部的代数式大于等于0，联立不等式组求得x的取值范围，用集合或区间表示后得到原函数的定义域．
解答：解：要使原函数有意义，则
，
由①得：x（x-1）＞0，即x＜0或x＞1，
由②得：x≥0．
所以x＞1．
所以原函数的定义域为（1，+∞）．
故选B．
|
由①得：x（x-1）＞0，即x＜0或x＞1，
由②得：x≥0．
所以x＞1．
所以原函数的定义域为（1，+∞）．
故选B．
点评：本题考查了函数的定义域及其求法，考查了分式不等式的解法，是基础题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
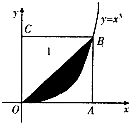（2013•临沂一模）如图所示，在边长为l的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（ ）
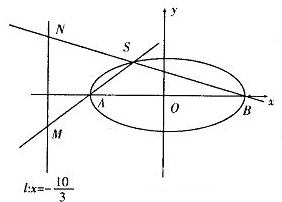（2013•临沂一模）如图，已知椭圆C：