题目内容
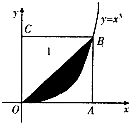 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )分析:欲求所投的点落在阴影部分内部的概率,须结合定积分计算阴影部分平面区域的面积,再根据几何概型概率计算公式易求解.
解答:解:由题意可知,此题求解的概率类型为关于面积的几何概型,
由图可知基本事件空间所对应的几何度量S(Ω)=1,
曲线y=x3与 y=x所围成的图形的面积S,即满足所取的点落在阴影部分内部所对应的几何度量:
S(A)=
(x-x3)dx=(
x2-
x4)|
=
.
则点M取自阴影部分的概率为P(A)=
=
.
故选B.
由图可知基本事件空间所对应的几何度量S(Ω)=1,
曲线y=x3与 y=x所围成的图形的面积S,即满足所取的点落在阴影部分内部所对应的几何度量:
S(A)=
| ∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 4 |
1 0 |
| 1 |
| 4 |
则点M取自阴影部分的概率为P(A)=
| S(A) |
| S |
| 1 |
| 4 |
故选B.
点评:本题考查了利用定积分求面积以及几何摡型知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
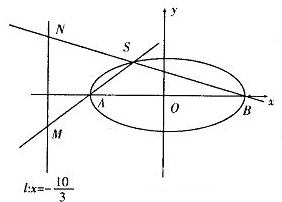 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: