题目内容
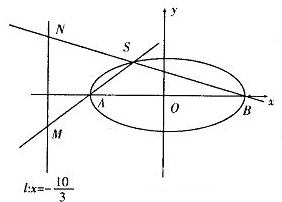 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 10 |
| 3 |
(I)求椭圆C的方程;
(Ⅱ)求线段MN长度的最小值;
(Ⅲ)当线段MN长度最小时,在椭圆C上是否存在这样的点P,使得△PAS的面积为l?若存在,确定点P的个数;若不存在,请说明理由.
分析:(I)由题意(0,b)在直线x-y+1=0上,代入解得b.再利用e=
,b2+c2=a2,解得a,c即可.
(II)设直线AS的斜率为k(k>0),则直线AS:y=k(x+2),与x=-
联立解得M,把直线y=k(x+2)与椭圆方程联立即可解得S,进而得到直线BS的方程,即可得出点N的坐标即|MN|,利用基本不等式的性质即可得出最小值;
(III)利用(II)可得k及点S的坐标,可得|AS|,可得AS方程为y=x+2,及P在与AS平行的直线y=x+m上.利用点到直线的距离公式及三角形的面积公式可得m,把直线y=x+m与椭圆的方程联立即可得出交点P的坐标.
| c |
| a |
(II)设直线AS的斜率为k(k>0),则直线AS:y=k(x+2),与x=-
| 10 |
| 3 |
(III)利用(II)可得k及点S的坐标,可得|AS|,可得AS方程为y=x+2,及P在与AS平行的直线y=x+m上.利用点到直线的距离公式及三角形的面积公式可得m,把直线y=x+m与椭圆的方程联立即可得出交点P的坐标.
解答:解:(I)由题意(0,b)在直线x-y+1=0上,代入解得b=1.
又∵e=
=
,b2+c2=a2,解得a=2,c=
.
∴椭圆C的方程为
+y2=1.
(II)由(I)A(-2,0),B(2,0).
设直线AS的斜率为k(k>0),则直线AS:y=k(x+2),与x=-
联立解得M(-
,-
).
由
,得(1+4k2)x2+16k2x+16k2-4=0.
∴xA•xS=-2xS=
,∴xS=
.
把xS代入y=k(x+2)得yS=
,即S(
,
).
∴kBS=
=-
.
∴直线BS的方程为y=-
(x-2),∴yN=-
(-
-2)=
,
∴|MN|=|yN-yM|=|
-(-
k)|=
|k+
|=
(k+
)≥
,当且仅当k=1时取等号.
(III)由(II)可知:k=1时线段MN取得最小值,此时S(-
,
),|AS|=
=
.
可得AS方程为y=x+2,P在与AS平行的直线y=x+m上.
∴点P到AS的距离等于两平行线距离
,∴△ASP的面积为1.
∴
×
×
=1,
∴|m-2|=
,解得m=-
或
.
又由
,得5x2+8mx+4m2-4=0,
△=(8m)2-4×5(4m2-4)=16(5-m2),
验证可知:当m=-
时,△=16×[5-(-
)2]=76>0.
∴P点存在,有两个.
又∵e=
| c |
| a |
| ||
| 2 |
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
(II)由(I)A(-2,0),B(2,0).
设直线AS的斜率为k(k>0),则直线AS:y=k(x+2),与x=-
| 10 |
| 3 |
| 10 |
| 3 |
| 4k |
| 3 |
由
|
∴xA•xS=-2xS=
| 16k2-4 |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
把xS代入y=k(x+2)得yS=
| 4k |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
∴kBS=
| ||
|
| 1 |
| 4k |
∴直线BS的方程为y=-
| 1 |
| 4k |
| 1 |
| 4k |
| 10 |
| 3 |
| 4 |
| 3k |
∴|MN|=|yN-yM|=|
| 4 |
| 3k |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| k |
| 4 |
| 3 |
| 1 |
| k |
| 8 |
| 3 |
(III)由(II)可知:k=1时线段MN取得最小值,此时S(-
| 6 |
| 5 |
| 4 |
| 5 |
(-2+
|
| 4 |
| 5 |
| 2 |
可得AS方程为y=x+2,P在与AS平行的直线y=x+m上.
∴点P到AS的距离等于两平行线距离
| |m-2| | ||
|
∴
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| |m-2| | ||
|
∴|m-2|=
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
又由
|
△=(8m)2-4×5(4m2-4)=16(5-m2),
验证可知:当m=-
| 1 |
| 2 |
| 1 |
| 2 |
∴P点存在,有两个.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立得到判别式及根与系数的关系、点到直线的距离公式、三角形面积计算公式等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
相关题目
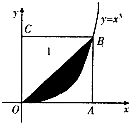 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )