题目内容
(本题满分16分)
已知函数![]() 是不同时为零的常数),其导函数为
是不同时为零的常数),其导函数为![]() 。
。
当a=![]() 时,若存在
时,若存在![]() ,使得
,使得![]() >成立,求b的取值范围;
>成立,求b的取值范围;
求证:函数y=![]() d (-1,0)内至少存在一个零点;
d (-1,0)内至少存在一个零点;
若函数f(x)为奇函数,且在x=1处的切线垂直于在线x+2y-3=0, 关于x的方程![]() 在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。
在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。
(1)当![]() 时,
时,![]() =
=![]() =
=![]() ,其对称轴为直线
,其对称轴为直线![]() ,
,
当![]() 解得
解得![]() ,当
,当![]()
![]()
![]() 无解,
无解,
所以![]() 的的取值范围为
的的取值范围为![]() .……………………………………………………………4分
.……………………………………………………………4分
(2)因为![]() ,
,
法一:当![]() 时,
时,![]() 适合题意.……………………………………………………………6分
适合题意.……………………………………………………………6分
当![]() 时,
时,![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,因为
,因为![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内有零点.
内有零点.
当![]() 时,
时,![]() ,所以
,所以![]() 在(
在(![]() 内有零点.
内有零点.
因此,当![]() 时,
时,![]() 在
在![]() 内至少有一个零点.
内至少有一个零点.
综上可知,函数![]() 在
在![]() 内至少有一个零点.…………………………………10分
内至少有一个零点.…………………………………10分
法二:![]() ,
,![]() ,
,![]() .
.
由于![]() 不同时为零,所以
不同时为零,所以![]() ,故结论成立.
,故结论成立.
(3)因为![]() =
=![]() 为奇函数,所以
为奇函数,所以![]() , 所以
, 所以![]()
![]() ,
,
又![]() 在
在![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 上是増函数,在
上是増函数,在![]() 上是减函数,由
上是减函数,由![]() 解得
解得![]() ,如图所示,
,如图所示,
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
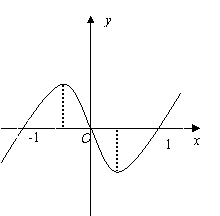 当
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,显然不成立;
时,显然不成立;
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,故
,故![]() .
.
所以所求![]() 的取值范围是
的取值范围是![]() ,或
,或![]() .
.
(以上各题如考生另有解法,请参照本评分标准给分)

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在