题目内容
(14分)一船由甲地逆水驶至乙地,甲、乙两地相距 S (km),水的流速为常量a(km/h),船在静水中的最大速度为b (km/h) (b>2a),已知船每小时的燃料费用(单位:元)与船在静水中的速度 v(km/h) 的平方成正比,比例系数为 k ,问:
(1)船在静水中的航行速度 v 为多少时,全程燃料费用最少?
(2)若水速 a =" 8.4" km/h,船在静水中的最大速度为b="25" km/h,要使全程燃料费用不超过40 k S元,求船在静水中的航行速度v 的范围。
(1)船在静水中的航行速度 v 为多少时,全程燃料费用最少?
(2)若水速 a =" 8.4" km/h,船在静水中的最大速度为b="25" km/h,要使全程燃料费用不超过40 k S元,求船在静水中的航行速度v 的范围。
(1)船在静水中速度 v =" 2a" (km/h)时,全程燃料费最少。
(2)当 12≤ v ≤ 25 时,全程燃料费不超过40kS元.
(2)当 12≤ v ≤ 25 时,全程燃料费不超过40kS元.
本试题主要是考查了函数在物理中的运用。
(1)根据已知中的条件可知设设全程燃料费用为 y,故全程所需时间为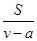
,那么y =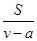 kv 2 ,进而得到解析式,,分析定义域和不等式的思想得到最值。
kv 2 ,进而得到解析式,,分析定义域和不等式的思想得到最值。
(2)由以知得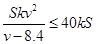 ,得到得
,得到得 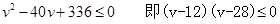 ,解不等式得到范围进而得到最值。
,解不等式得到范围进而得到最值。
解:(1)设全程燃料费用为 y . …… 1分
∵ 全程所需时间为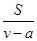
∴ y =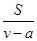 kv 2 ……2分
kv 2 ……2分
=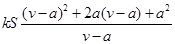 ……3分
……3分
=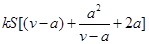 v∈( a , b ] ……4分
v∈( a , b ] ……4分
∵ v – a > 0 ∴ y≥ 4akS , …… 5分
当且仅当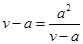 , 即 v =" 2a" 时取等号,……6分
, 即 v =" 2a" 时取等号,……6分
∵ 2a ∈ ( a, b ] ( 7分) ∴ 当 v = 2a时,全程燃料费最少. ……8分
(2) 由以知得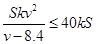 ……10分
……10分
得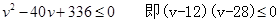 12 ≤ v ≤ 28 .
12 ≤ v ≤ 28 .
∵v ≤ b 12≥a ∴ 12 ≤ v ≤ 25 ……13分
答 (1)船在静水中速度 v =" 2a" (km/h)时,全程燃料费最少。
(2)当 12≤ v ≤ 25 时,全程燃料费不超过40kS元. ……14分
(1)根据已知中的条件可知设设全程燃料费用为 y,故全程所需时间为
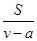
,那么y =
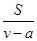 kv 2 ,进而得到解析式,,分析定义域和不等式的思想得到最值。
kv 2 ,进而得到解析式,,分析定义域和不等式的思想得到最值。(2)由以知得
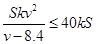 ,得到得
,得到得 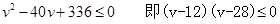 ,解不等式得到范围进而得到最值。
,解不等式得到范围进而得到最值。解:(1)设全程燃料费用为 y . …… 1分
∵ 全程所需时间为
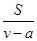
∴ y =
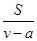 kv 2 ……2分
kv 2 ……2分=
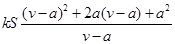 ……3分
……3分=
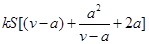 v∈( a , b ] ……4分
v∈( a , b ] ……4分∵ v – a > 0 ∴ y≥ 4akS , …… 5分
当且仅当
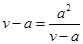 , 即 v =" 2a" 时取等号,……6分
, 即 v =" 2a" 时取等号,……6分∵ 2a ∈ ( a, b ] ( 7分) ∴ 当 v = 2a时,全程燃料费最少. ……8分
(2) 由以知得
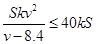 ……10分
……10分得
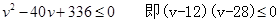 12 ≤ v ≤ 28 .
12 ≤ v ≤ 28 . ∵v ≤ b 12≥a ∴ 12 ≤ v ≤ 25 ……13分
答 (1)船在静水中速度 v =" 2a" (km/h)时,全程燃料费最少。
(2)当 12≤ v ≤ 25 时,全程燃料费不超过40kS元. ……14分

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
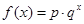 ;②
;②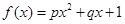 ;③
;③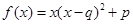 .(以上三式中、
.(以上三式中、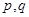 均为常数,且
均为常数,且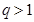 )
)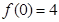 ,
,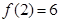 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是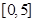 .其中
.其中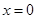 表示8月1日,
表示8月1日,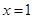 表示9月1日,…,以此类推);
表示9月1日,…,以此类推); ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;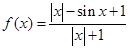
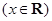 的最大值为
的最大值为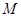 ,最小值为
,最小值为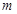 ,则
,则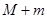 的值为 .
的值为 .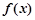 =(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则
=(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则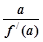 +
+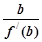 +
+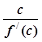 等于( )
等于( )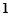
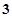
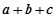
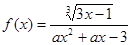 的定义域是
的定义域是 , 则实数
, 则实数 的取值范围是___________.
的取值范围是___________. 的最小值为
的最小值为 ,则
,则