题目内容
9.函数f(x)=lg(2x-3)的定义域是( )| A. | [$\frac{3}{2}$,+∞) | B. | ($\frac{3}{2}$,+∞) | C. | (-∞,$\frac{3}{2}$] | D. | (-∞,$\frac{3}{2}$) |
分析 根据对数函数的性质得到关于x的不等式,解出即可.
解答 解:由题意得:2x-3>0,
解得:x>$\frac{3}{2}$,
故选:B.
点评 本题考查了函数的定义域问题,是一道基础题.

练习册系列答案
相关题目
17.如图所示的程序框图,运行后输出结果为( )
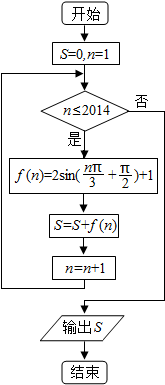

| A. | 2017 | B. | 4028 | C. | 2014 | D. | 2011 |
4.若函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{π,x=0}\\{0,x<0}\end{array}\right.$,则f{f[f(-2)]}=( )
| A. | 0 | B. | π | C. | π2 | D. | 4 |
18.等差数列{an}中,a4=9,则前7项的和S7=( )
| A. | $\frac{63}{2}$ | B. | 28 | C. | 63 | D. | 36 |