题目内容
19.设抛物线y2=12x的焦点为F,经过点P(2,1)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则|AF|+|BF|=( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 求出焦点坐标和准线方程,过A、B、P 作准线的垂线段,垂足分别为 M、N、R,利用抛物线的定义得到|AM|
+|BN|=2|PR|,求得结果.
解答 解:抛物线 x2=12y的焦点为F(0,3),准线方程为y=-3,过A、B、P 作准线的垂线段,
垂足分别为 M、N、R,
点P恰为AB的中点,故|PR|是直角梯形AMNB的中位线,故|AM|+|BN|=2|PR|.
由抛物线的定义可得|AF|+|BF|=|AM|+|BN|=2|PR|=2|1-(-3)|=8,
故选:B.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,利用抛物线的定义得到|AM|+|BR|=2|PN|,是解题的关键.

练习册系列答案
相关题目
9.某程序框图如图所示,当输出y值为-8时,则输出x的值为( )
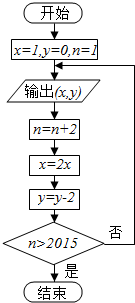

| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
10.已知点 P(3,4),Q(2,6),向量$\overrightarrow{{E}F}=({-1,λ})$.若$\overrightarrow{{P}Q}∥\overrightarrow{{E}F}$,则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
14.若tan(θ+$\frac{π}{4}$)=-3,则$\frac{sin2θ}{1+cos2θ}$=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
11.直线$\sqrt{3}$x+3y+1=0的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
8.“0<a<4”是“命题“?x∈R,不等式x2+ax+a≥0成立,为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.函数f(x)=lg(2x-3)的定义域是( )
| A. | [$\frac{3}{2}$,+∞) | B. | ($\frac{3}{2}$,+∞) | C. | (-∞,$\frac{3}{2}$] | D. | (-∞,$\frac{3}{2}$) |