题目内容
已知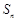 是等比数列
是等比数列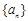 的前
的前 项和,
项和,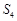 、
、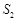 、
、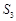 成等差数列,且
成等差数列,且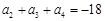 .
.
(1)求数列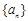 的通项公式;
的通项公式;
(2)是否存在正整数 ,使得
,使得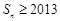 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
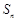 是等比数列
是等比数列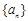 的前
的前 项和,
项和,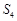 、
、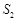 、
、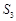 成等差数列,且
成等差数列,且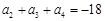 .
.(1)求数列
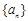 的通项公式;
的通项公式;(2)是否存在正整数
 ,使得
,使得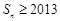 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.(1)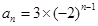 ;(2)存在符合条件的正整数
;(2)存在符合条件的正整数 的集合为
的集合为 .
.
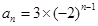 ;(2)存在符合条件的正整数
;(2)存在符合条件的正整数 的集合为
的集合为 .
.试题分析:(1)设数列
 的公比为
的公比为 ,依题意,列出关于首项
,依题意,列出关于首项 与公比
与公比 的方程组,解之即可求得数列
的方程组,解之即可求得数列 的通项公式;(2)依题意,可得
的通项公式;(2)依题意,可得 ,对
,对 的奇偶性进行分类讨论,即可求得答案.
的奇偶性进行分类讨论,即可求得答案.试题解析:(1)解:设数列
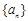 的公比为
的公比为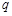 ,则
,则 ,
,
由题意得
 即
即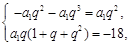 解得
解得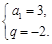
故数列
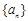 的通项公式为
的通项公式为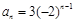 6分
6分(2)由(1)有
 7分
7分若存在
 ,使得
,使得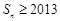 ,则
,则 ,即
,即 8分
8分当
 为偶数时,
为偶数时,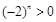 ,上式不成立 9分
,上式不成立 9分当
 为奇数时,
为奇数时, ,即
,即 ,则
,则 11分
11分综上,存在符合条件的正整数
 的集合为
的集合为 12分.
12分.
练习册系列答案
相关题目
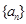 的公比为q,且
的公比为q,且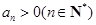 ,
,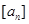 表示不超过实数
表示不超过实数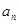 的最大整数(如
的最大整数(如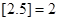 ),记
),记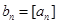 ,数列
,数列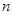 项和为
项和为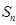 ,数列
,数列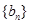 的前
的前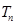 .
.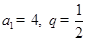 ,求
,求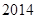 的正整数n,都有
的正整数n,都有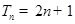 ,证明:
,证明: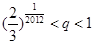 .
.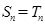 (
(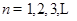 )的充分必要条件为
)的充分必要条件为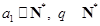 .
.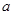 为实数,数列
为实数,数列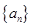 满足
满足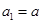 ,当
,当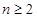 时,
时,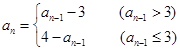 ,
, 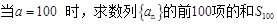 ;(5分)
;(5分)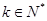 ,使
,使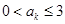 ;(5分)
;(5分)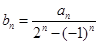 ,当
,当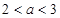 时,求证:
时,求证: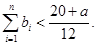 (6分)
(6分)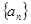 的各项都是正数,且
的各项都是正数,且 =16,则
=16,则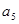 =( ).
=( ).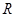 上的函数
上的函数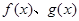 满足
满足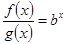 ,且
,且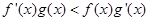 ,
, 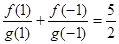 ,若
,若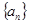 是正项等比数列,且
是正项等比数列,且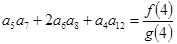 ,则
,则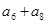 等于 .
等于 .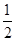 ,a4=-4,则|a1|+|a2|+…+|an|=________.
,a4=-4,则|a1|+|a2|+…+|an|=________.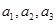 的和为定值
的和为定值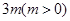 ,且公比为
,且公比为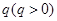 ,令
,令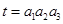 ,则
,则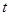 的取值范围为( )
的取值范围为( )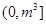
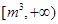
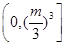
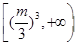
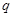 不为1的等比数列
不为1的等比数列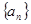 满足
满足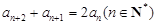 ,则
,则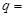 .
.