Question

在平面直角坐标系xOy中，已知点A（0，2），B（-2，0），C（1，0），分别以△ABC的边AB，AC向外作正方形ABEF与ACGH，则直线FH的一般式方程为

x+4y-14=0

．

Answer 1

分析：分别过H、F作y轴的垂线，垂足分别为M、N．根据正方形的性质证出Rt△AHM≌Rt△CAO，利用对应边相等及A、C两点的坐标，算出H（2，3），同理得到F（-2，4）．由此算出直线FH的斜率，利用直线方程的点斜式列式，化简即可得到直线FH的一般式方程．

解答：解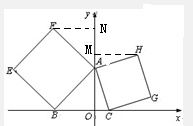：分别过H、F作y轴的垂线，垂足分别为M、N，
∵四边形ACGH为正方形，
∴Rt△AHM≌Rt△CAO，可得AM=OC，MH=OA，
∵A（0，2），C（1，0），
∴MH=OA=2，AM=OC=1，可得OM=OA+AM=3，
由此可得H坐标为（2，3），同理得到F（-2，4）
∴直线FH的斜率为k=

4-3

-2-2

=-

1

4

，
可得直线FH的方程为y-3=-

1

4

（x-2），化简得x+4y-14=0．
故答案为：x+4y-14=0

点评：本题给出顶点A、B、C在坐标轴上的两个正方形ABEF与ACGH，在已知A、B、C的坐标情况下求直线FH的方程．着重考查了正方形的性质、全等三角形的判定与性质、直线的基本量与基本形式等知识，属于中档题．