题目内容
对于三次函数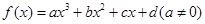 ,给出定义:设
,给出定义:设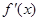 是函数
是函数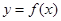 的导数,
的导数,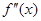 是
是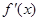 的导数,若方程
的导数,若方程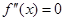 有实数解
有实数解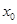 ,则称点
,则称点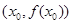 为函数
为函数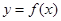 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”应对对称中心.根据这一发现,则函数
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”应对对称中心.根据这一发现,则函数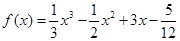 的对称中心为 .
的对称中心为 .
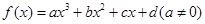 ,给出定义:设
,给出定义:设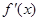 是函数
是函数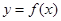 的导数,
的导数,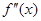 是
是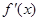 的导数,若方程
的导数,若方程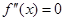 有实数解
有实数解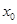 ,则称点
,则称点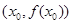 为函数
为函数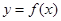 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”应对对称中心.根据这一发现,则函数
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”应对对称中心.根据这一发现,则函数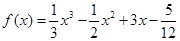 的对称中心为 .
的对称中心为 .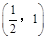
试题分析:由
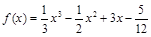 ,得
,得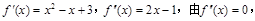
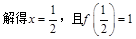 ,所以此函数的对称中心为
,所以此函数的对称中心为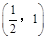 .
.点评:对于函数新概念问题,要根据函数的新定义及所学公式综合求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
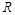 上的可导函数
上的可导函数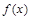 ,若满足
,若满足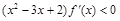 ,则在区间[1,2]上必有( )
,则在区间[1,2]上必有( )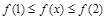
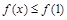
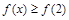
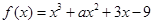 在
在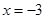 处取得极值
处取得极值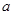 值
值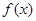 的单调递增区间.
的单调递增区间. 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; ,不等式
,不等式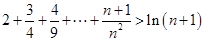 都成立.
都成立. ,
, ,其中
,其中 R .
R . 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; , 当
, 当 时,若存在
时,若存在 ,对于任意的
,对于任意的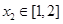 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.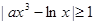 对任意
对任意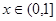 都成立,则实数a取值范围是 。
都成立,则实数a取值范围是 。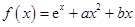 .
.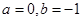 时,求
时,求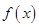 的单调区间;
的单调区间;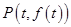
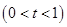 处的切线为
处的切线为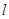 ,直线
,直线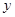 轴相交于点
轴相交于点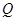 .若点
.若点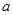 的取值范围.
的取值范围.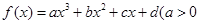 的零点的集合为{0,1},且
的零点的集合为{0,1},且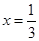 是f(x)的一个极值点。
是f(x)的一个极值点。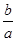 的值;
的值;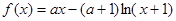 ..
..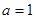 时,求
时,求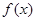 的单调区间;
的单调区间;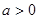 时,设
时,设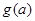 ,若
,若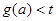 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.