题目内容
【题目】已知椭圆
的离心率为
，椭圆短轴的一个端点与两个焦点构成的三角形的面积为
.
（1）求椭圆
的方程式；
（2）已知动直线
与椭圆相交于
两点.
①若线段
中点的横坐标为
，求斜率
的值；
②已知点
，求证：
为定值.
【答案】（1）
＋
＝1
（2）①±
②见解析
【解析】
(1)
＋
＝1(a>b>0)满足a2＝b2＋c2，又
＝
，
×b×2c＝
，
解得a2＝5，b2＝
，则椭圆方程为＋＝1．
(2)设A(x1，y1)，B(x2，y2)．
①将y＝k(x＋1)代入＋＝1，
得(1＋3k2)x2＋6k2x＋3k2－5＝0，
∴Δ＝48k2＋20>0，x1＋x2＝－
，
∵AB中点的横坐标为－，
∴－＝－1，解得k＝±．
②由(1)知x1＋x2＝－，x1x2＝
，
∴
·
＝(x1＋
，y1)·(x2＋，y2)
＝(x1＋)(x2＋)＋y1y2
＝(x1＋)(x2＋)＋k2(x1＋1)(x2＋1)
＝(1＋k2)x1x2＋(＋k2)(x1＋x2)＋
＋k2
＝(1＋k2)＋(＋k2)(－)＋＋k2
＝
＋＋k2＝
(定值)．
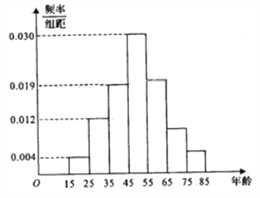
【题目】2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策，为了了解适龄民众对放开生育二胎政策的态度，某市进行了一次民意调查，参与调查的100位市民中，年龄分布情况如下图所示，并得到适龄民众对放开生育二胎政策的态度数据如下表：
生二胎 | 不生二胎 | 合计 | |
25~35岁 | 10 | ||
35~50岁 | 30 | ||
合计 | 100 |
（1）填写上面的
列联表；
（2）根据调查数据，有多少的把握认为“生二胎与年龄有关”，说明理由；
（3）调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子，各自家庭都有一个约定：父亲先生二胎，然后儿子生二胎，则这三个家庭“二胎出生的日期的先后顺序”有多少种？
参考数据：
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
（参考公式：
，其中
）
【题目】刘老师是一位经验丰富的高三理科班班主任，经长期研究，他发现高中理科班的学生的数学成绩（总分150分）与理综成绩（物理、化学与生物的综合，总分300分）具有较强的线性相关性，以下是刘老师随机选取的八名学生在高考中的数学得分x与理综得分y（如下表）：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理综分数y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
参考数据及公式： 
．
（1）求出y关于x的线性回归方程；
（2）若小汪高考数学110分，请你预测他理综得分约为多少分？（精确到整数位）；
（3）小金同学的文科一般，语文与英语一起能稳定在215分左右．如果他的目标是在
高考总分冲击600分，请你帮他估算他的数学与理综大约分别至少需要拿到多少分？（精确到整数位）．
【题目】为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表和频率分布直方图：
月工资 （单位：百元） | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
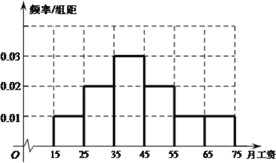
(1)
试由上图估计该单位员工月平均工资；
(2)现用分层抽样的方法从月工资在
和
的两组所调查的男员工中随机选取5人，问各应抽取多少人？
(3)若从月工资在
和两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．