Question

【题目】2017年天猫五一活动结束后，某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况，随机在当地消费超过3000元的群众中抽取了500人作调查，所得概率分布直方图如图所示：记年龄在， ， 对应的小矩形的面积分别是，且.

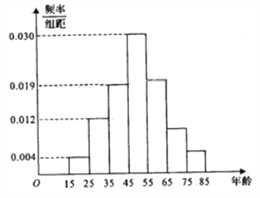
（1）以频率作为概率，若该地区五一消费超过3000元的有30000人，试估计该地区在五一活动中消费超过3000元且年龄在的人数；

（2）若按照分层抽样，从年龄在的人群中共抽取6人，再从这6人中随机抽取2人作深入调查，求至少有1人的年龄在内的概率.

Answer 1

【答案】（1）15000（人）；（2）.

【解析】试题分析：

(1)由频率分布直方图可得年龄在的人数为15000人；

(2)利用题意结合古典概型公式可得：至少有1人的年龄在内的概率为 .

试题解析：

（1）设区间的频率为x，则区间内的频率依次为，依题意得

在五一活动中消费超过3000元且年龄在岁之间的人数为：

（人）

（2）若按分层抽样，年龄在分别抽取2人和4人，记年龄在的两

人为A,B，记年龄在的4人为1，2，3，4；随机抽取两人可能情况有：

(A,B),(A,1)(A,2),(A,3),(A,4),(B,1),(B,2),(B,3),(B,4),(1,2),(1,3),(1,4)，(2,3),(2,4),(3,4),共15种情况，

其中满足条件的有：(A,B),(A,1)(A,2),(A,3),(A,4),(B,1),(B,2),(B,3),(B,4)共9

种故所求概率为： .